Justamente ayer se me ocurrió consultar en Tiobe los lenguajes más 'populares' (esto tiene cierta acotación, ver nota al final), del 2023, y claramente C aparece en 2ª posición, C++ en 3ª y C# en 5ª...    cita hasta 100, aunque solo da datos de los 50 primeros

Esta imagen es una captura de techrepublic (sobre la página de Tiobe) de solo los 10 primeros:


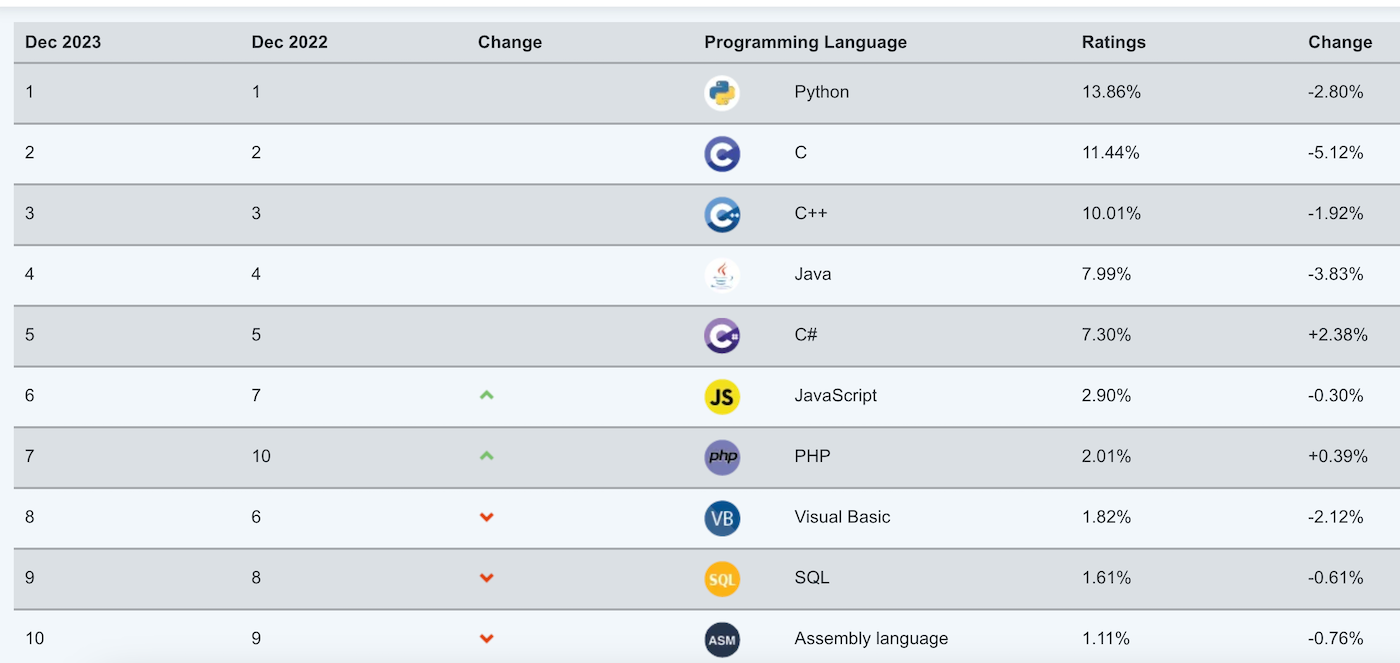
https://www.tiobe.com/tiobe-index/


Lo que tu amiga quizás quiso decirte es que en un entorno de computación cuántica, no usan C, probablemente muchos d elos lenguajes existentes, tendrán serias limitaciones en esos entornos, y es más que probable que opten por usar alguno lo más flexible posible que se pueda adaptar rápidamente a como ellos evolucionan, para no perder tiempo también con esto. En ese sentido, lenguajes interpretados les facilita probar parcialmente y corregir (interrumpir y seguir diseñando) sin perder tiempo en compilar y probar cada vez.

nota: El índice TIOBE es un indicador de la popularidad de los lenguajes de programación. Se actualiza una vez al mes. Las calificaciones se basan en el número de ingenieros cualificados en todo el mundo, cursos y proveedores de terceros, motores de búsqueda populares como Google, Bing, Yahoo, Wikipedia, Amazon, YouTube y Baidu se utilizan para calcular las calificaciones. Es importante señalar que el índice TIOBE no trata del "mejor lenguaje de programación" ni de "el lenguaje en que se han escrito más líneas de código".

Gracias   .

...copiaré el magnet, y desempolvaré el bittorrent...

...Descargando... 

No sé si me has entendido del todo... pareciera que dices que por habilitar una política tenga que generarse un valor único en el registro, y no es eso lo que yo te estoy diciendo.

Yo te digo que apliques un valor único (desde el editor de políticas) a una clave y la guardes, aunque no sepas donde se guardó en el registro, se usará luego ese valor único para localizar la clave en el registro.

Si pones un valor string, por ejemplo:  "xgggg999ssstgppppwww222rmdhtttyyyX"
Va a ser que ese valor no existe en el registro, luego si copias el valor que supuestamente has puesto(desde el editor de políticas) como esperando que sea único (si no fuera único aparecerá muchas veces), solo la clave que buscas es la que contendrá ese valor... al localizarlo, estás teniendo la ruta hacia dicha clave.

Nota sin embargo que determinadas claves se repiten tipo de 'users' en 'current_user' o de 'local_machine' en 'current_config'... así si es el caso podrías ver que al buscarla aparece en 2 sitios...

El sistema es sencillo y fácil de entender y aplicar.

Haz un cambio pon un valor característico, que sea identificativo para ti y nadie más (o sea, un valor único)... guárdalo (me refiero operando desde el editor de políticas).
Luego vas al registro y pones a buscar el valor (se supone que es único) que has establecido... si fue bien, lo encontrará y entonces tendrás ante tí la ruta exacta hacia la clave deseada.
Es de suponer que todas las otras claves que vayas a manejar sean 'hernanas' de esta.
Acuérdate de volver a restablecer el valor previo tras encontrar la ruta.

Yo lo pondría en un tabulador de fichas.
Cada apartado en una ficha, la primera por supuesto "general features".

Respecto del gridview, dado que al pulsar en una fila ofrece detalles (no sé si en ventana emergente, o al pide de la ventana), yo haría el control más esteecho, para que ambas columnas ("Master y Slave datagram"), no ocuparan más de lo que actualmente ocupa una.

En "General Status", añadidiría un checkbox informativo para indicar si está o no conectado a un TPV, y en caso afirmativo un botón para mostrar opciones 'extended' que contemplas.

En el "Network Map", el state se muestra con un color, debajo del gridview, sería acertado una leyenda que explicara cada color.

Me pasa igual ningún enlace es válido a día de hoy...

me quedé sin bajarlo en su momento a la espera de liberar espacio en el portátil...y al final olvidé el tema.

Si algún alma caritativa lo repone o tiene un enlace de descarga válido al de 42Gb. que lo pase por aquí

La solución es comprar la licencia de uso del programa.
A ti te gustaría que la gente pudiera adquirir tus productos sin pagarlos????.

Pues si te resulta interesante las cadenas de Markov, te recomiendo que explores el algoritmo de Viterbi... que trata precisamente con modelos ocultos de Markov (HMM).

Es raro eso de que "la potencia funciona mal"... un lenguaje puede tener bugs, pero nunca tan evidentes que no fueran corregidos.

En cualquier caso, una potencia es una serie de mutiplicaciones, luego ejecuta un bucle.

Potencia              Bucle
---------------------------------------
10^0 =1
10^1 = 10    
10^2 = 100   ---->10x10
10^3 = 1000 ----> 10x10x10
10^4 = 10000 ----> 10x10x10x10
...

Al final restas 1 y ya tienes todos los 9...
los caso 0 y 1 puedes tratarlos en un 'else'


p.d.: Más aún antes del bucle puede condicionarse para los casos 0 y 1. Aunque el código en ambos casos no difiere mucho en cuanto a la ncantidad de líneas de código...

Sí, yo tengo varios libros... pero también en pdf y algún compilador creo recordar...
Dame tiempo que los busque y de aquí al sábado los suba al servidor del foro.


Como un vistazo rápido:
- Se empezó con lo que fue el estándar de ADA (todo un culebrón venezolano desde que el DoD lanzó su oferta), ADA83. Es imprescindible el libro: ADA: Language, compilers and Bibliography - ISBN:0521264642. En él viene la especificación del lenguaje recogida de forma exhaustiva. En la segunda parte del libro (hojas en verde), viene una extensa bibliografía (unas 25 páginas con unas 12 referencias por cada).
- Luego en 1987 se hiizo una revisión que se aprobó.
- En 1995 se hizo una versión nueva, conocida como ADA95. De aquí se hizo también un compilador con POO... debería tenerlo en algún disco.
- Se actualizó en 2005, 2012 y creo que recientemente en 2022.