Escriba un programa que estime el valor de la constante matemática e, mediante el uso de la fórmula:

 e = 1 + 1/1! + 1/2! + 1/3! + ...

Necesito que me corrijan si entendí bien, bueno, para empezar no recuerdo haber visto lo de la constante "e" en la preparatoria o al menos creo que la vi un poco en temas de derivadas, pero en fin, nunca la estudie muy a fondo, así que cuando lei la definición en la wikipedia me sentí deslumbrado por la cantidad de conceptos que no entiendo, y por lo tanto me di cuenta de mi falta de conocimiento teórico  en matemáticas, bueno según a lo que yo entiendo tengo que sacar el valor de "e" que es aproximadamente : 2,7182818284590452..., mediante la formula que va en ascenso, es decir después de 1/3! sigue el 1/4! y así sucesivamente hasta que el resultado de un numero aproximado a e?.

para hacerlo no es tan complicado, muestra algo de progreso si quieres recibir algo de ayuda real...


si quieres hacerlo en alta precisión (miles o millones de decimales) aquí un tema con un poco de eso

Calculo de pi en alta precisión (aporte)

El número 'e' es el límite de la sucesión:

a_n= (1+1/n)ⁿ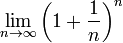




luego es:

e= lim (1+1/n)ⁿ  -> cuando n tiende a infinito

De modo que cuanto mayor sea el valor de N más exacto será el valor de  'e'. Por ejemplo:

(1 + 1/100)¹⁰⁰= 2.7048138294031855135...
(1 + 1/1000)¹⁰⁰⁰= 2.7169239326424202463...
(1 + 1/10000)¹⁰⁰⁰⁰= 2.7181459268252250988...
(1 + 1/100000)¹⁰⁰⁰⁰⁰=2.7182682371744897556...
(1 + 1/1000000)^1000000=2.7182804693193768982...
(1 + 1/10000000)^10000000=2.7182816925449640074...
...


Solamente se puede tener el número aproximado pues es un número irracional.

Si usas programas de cálculo, es posible que si da un número muy elevado a N te de como resultado 1 y no 2,71....

También sirve: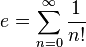



Aquí te dejo una manera de hacerlo con VB6, tendrás que pasarlo a C

Private Sub Command1_Click()
Dim e As Variant
Dim i As Variant
For i = 0 To (100)
e = e + (1 / Factorial(i))
Next i
Print e
End Sub
 
Private Sub Command2_Click()
Dim e As Variant
e = (1 + 1 / 10000000000#) ^ 10000000000#
Print e
End Sub
 
Public Function Factorial(NumFactorizar As Variant) As Variant
Dim X As Variant
X = NumFactorizar
For i = 1 To NumFactorizar - 1
X = X * (NumFactorizar - i)
Next i
If X = 0 Then X = 1
Factorial = X
End Function
 

Seguramente haya una manera mejor, pero espero que te sirva de idea

Hola,
El sábado estaba algo aburrido y me propuse averiguar otra forma de obtener el número e o base de los logaritmos naturales. Mi objetivo era obtener algo así:

2.718281828458563411277850606202642376785584483618617451918618203875586213119643873179950822014292195

Pero no lo he conseguido. Sin embargo he podido reducir la forma de calcularlo que puse en mi ejemplo anterior, eliminando la función "Factorial":

Dim e As Double
Dim X As Integer
Dim Fact As Double
Fact = 1
    For X = 0 To 100
        If X > 0 Then Fact = Fact * CDbl(X)
            e = e + (1 / Fact)
    Next X
 
Print e