deja claro que el siguiente tema no lo hago en pro de discutir la naturaleza de pi, ni nada al respecto, es solo en pro del calculo de alta precisión

aquí básicamente solo hay 2 temas importantes que abordar
-¿qué formula usar?
-¿como calculo números en alta precisión?
con lo primero... la formula, decidí usar la de euler

escogí esta por su precisión y su relativamente fácil aplicación
para aplicarla la tenemos que separar en 2 partes por su sumatoria y su factorial...
Código
ahí resolvemos esa formula básicamente... pero nos damos cuenta de un problema... los numeros double están limitados a 64 bits... unos 20 decimales para nuestro caso...
en este caso viene la aritmetica de alta precisión, GMP... aquí en el foro buscaba como usarlo... al final conseguí y publiqué el como...
este usa unidades especificas y operaciones especificas para alta precisión...
doy una ligera explicación de lo usado... no voy a caer en mucho detalle de las funciones...
mpf_t es una variable de tipo "float" propia
mpf_set_default_prec da el valor en bytes que la variable usará
mpf_init_set_str inicializa las variables desde un string... por que un string? porque quise -.-... se hay que inicializar las variables obligatoriamente
mpf_set_ui da un valor desde un entero sin signo a un float
div= division, mul = multiplicaccion, add= adición
mpf_get_str convierte de float de GMP a char* (string)
como no habia una multiplicacion / asignacion directa, me tocó usar una variable de intercambio
ahora la parte interesante... el codigo

hice un pequeño/bonito formato de impresión de 10 en 10 dígitos... en lineas de 50 y bloques de 500 con el numero de dígito como indicador... probé solo hasta 40.000 dígitos, comprobando en internet precisos... pero en 5min 9 seg!
 es mi único intento en este campo... no esperen romper el record mundial de decimales ;P por cierto... de ahí en adelante, los dígitos son cuesta arriba... así que cuidado con el tiempo... pueden usar el programa pasando el numero de dígitos como argumento... los dígitos los toma en cuanta de 100 en 100
es mi único intento en este campo... no esperen romper el record mundial de decimales ;P por cierto... de ahí en adelante, los dígitos son cuesta arriba... así que cuidado con el tiempo... pueden usar el programa pasando el numero de dígitos como argumento... los dígitos los toma en cuanta de 100 en 100pd: la precisión la hago como "precision = digitos * 100 * 3 * 1.12" porque descubrí que se requieren 3 ciclos por dígito correcto sobre los 100 con un 12% de error (calculado a ojo)

---------------------------------------------------------------codigo final con formulas a partir de aqui---------------------------------------------------------------
librerias
Código
prototipos
Código
main
Código
tiene 2 argumentos... primero los digitos (obligatorio)... luego -r para ramanujan o -e para euler (opcional, euler predeterminado)
imprimir_pi_aux
para tener un formato único de impresión para todo
Código
aux por consejo de amchacon
metodo_euler
corto, simple, pero largo... para 10.000 dígitos 33.600 ciclos o para mi unos 11 seg
basado en la formula

Código
metodo_ramanujan
por consejo de do-while, basado en la formula
eficiente, pero dificil de aplicar (si no, miren el codigo de abajo)
para 10.000 digitos 1.262 ciclos en 1.1 segundos
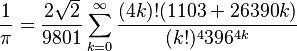
Código





 Autor
Autor



 En línea
En línea
















