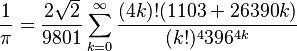do-while: lo que es la arrogancia! XD al final si era el factorial el error! XD (eso creo)
XD pero ahorita está más feo aún pero funciona! y es increiblemente eficiente!
de ahora en adelante publicaré el codigo en el post inicial... no lo publicaré como un gran bloque sino, cada sección... olvidense de imprimir en archivo y de la modularidad! XD eso aún lo postergo
Gh057: lo había visto! XD pero me tomará otro dia adaptarlo, aunque como tiene similaridad con Ramanujan no se me debría ser tan difícil...
alguna vez vi algo de comentario de código cómicos... este merece uno que vi
aqui la correccion de Ramanujan
si no fuera tan flojo (y estuviera claro en el tema), intentara hacer operator overload para usar los operadores normales! D:
a partir de ahora modifico el post principal
XD pero ahorita está más feo aún pero funciona! y es increiblemente eficiente!
de ahora en adelante publicaré el codigo en el post inicial... no lo publicaré como un gran bloque sino, cada sección... olvidense de imprimir en archivo y de la modularidad! XD eso aún lo postergo
Gh057: lo había visto! XD pero me tomará otro dia adaptarlo, aunque como tiene similaridad con Ramanujan no se me debría ser tan difícil...
alguna vez vi algo de comentario de código cómicos... este merece uno que vi
Código
aqui la correccion de Ramanujan
Código
si no fuera tan flojo (y estuviera claro en el tema), intentara hacer operator overload para usar los operadores normales! D:
a partir de ahora modifico el post principal
Disculpa por revivir el post. Muy buen post, en definitiva Pi tiene muchos decimales, que en calculos escolares me basta con 3.1416 xD, Pero jamás entendí la ecuacuón de Ramanujan.
Me volví loco y opté por enender otras, ¿me la puedes explicar con peras y manzanas?

Un Cordial Saludo






 Autor
Autor



 En línea
En línea