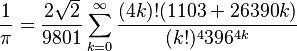Autor Autor
|
Tema: Calculo de pi en alta precisión (aporte) (Leído 17,291 veces)
|
do-while
 Desconectado Desconectado
Mensajes: 1.276
¿Habra que sacarla de paseo?

|
¡Buenas! Si te interesa el tema de pi, hay por ahí una formula de Ramanujan que calcula 8 decimales por iteración (era un fiera). ¡Saludos!
|
|
|
|
|
 En línea
En línea
|
- Doctor, confundo los números y los colores.
- Vaya marrón.
- ¿Marrón? ¡Por el culo te la hinco!
|
|
|
|
engel lex
|
gracias do-while!  vamos con esa! voy a extender el programa... ya llegué a mi casa, tengo 1,5l de te negro listos y 250g de maní japonés! ese código sale en un rato! 
|
|
|
|
|
 En línea
En línea
|
El problema con la sociedad actualmente radica en que todos creen que tienen el derecho de tener una opinión, y que esa opinión sea validada por todos, cuando lo correcto es que todos tengan derecho a una opinión, siempre y cuando esa opinión pueda ser ignorada, cuestionada, e incluso ser sujeta a burla, particularmente cuando no tiene sentido alguno.
|
|
|
1mpuls0
 Desconectado Desconectado
Mensajes: 1.186

|
próximo a probar:salida concatenada a archivo, tiempo de ejecución, alguna sugerencia?
No sé mucho de c++, apenas estoy en pañales pero tal vez esto te pueda servir. De hecho la idea viene de un programa que hice en otro lenguaje pero tratando de implementarlo en c++, aunque tal vez necesitas algo más "exacto" (microsegundos, aunque creo que los ordenadores no trabajan a ese nivel) Además parece haber un fallo en mi método xD #include <iostream> #include <ctime> using namespace std; int main() { clock_t tiempo_inicial = clock(); //Alguna función for(int indice=0;indice<=10000;indice=indice+1) { std::cout << indice << endl; } clock_t tiempo_final = clock(); std::cout << float( tiempo_final - tiempo_inicial ) / CLOCKS_PER_SEC << " segundos"; return 0; }
Lo que me causa intriga es lo siguiente:  ....
10000
1.283 segundos
Process returned 0 (0x0) execution time : 1.323 s
|
|
|
|
|
 En línea
En línea
|
abc
|
|
|
|
engel lex
|
la ecuación de Ramanujan es una locura @.@ es un poco dificil de aplicar... sin embargo dudo de su eficiencia al momento de procesar, ya que a diferencia de la de euler es muy compleja, tiene 2 factoriales diferentes (y el de arriba es grande, con k = 3 el valor es de 479.001.600) la de abajo tiene 2 potencias y la segunda es de 4*k, haciéndola sin funciones matemáticas precompiladas sería for(i=1;i<precision;i++){ for(j=1;j<=4*i;j++){ factorial1*=j; } for(j=1;j<=i;j++){ factorial2*=j; } for(j=1;j<=4;j++){ factorial2*=factorial2; } for(j=1;j<=4*i;j++){ divisor*=396; } sumatoria+=(factorial1*(1103+26390*i))/(factorial2*divisor) } sumatoria=1/sumatoria
el código sobre eso se puede optimizar pero igual son muchos ciclos dentro de cada ciclo (cuando precision = 1.000; tendrá que hacer por lo menos 4.000.000 de ciclos secundarios los cuales multiplicarán valores muy grandes, esto sin contar que sería solo para obtener 8.000 dígitos teóricos...) la de euler es simple y hasta bonita XD solo requiere en ciclo principal y unas pocas operaciones aqui la formula de Ramanujan 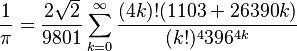 cambié un poco el programa para hacerlo más modular... ya se me hizo tarde... así que ni argumentos (más que ramanujan), ni corrida silenciosa, ni salida a archivo!  sorry por ahora... estoy cansado  agregado por ahora, ramanujan (no da pi... si alguien me ayuda con esto, sobre donde me equivoco...), tiempo de calculo e impresion por cierto amchacon sobre el tiempo de impresión incluso a 40.000 decimales la diferencia es instrumental, no llega al medio segundo de diferencia  aquí el código... se está tornando largo D: #include <iostream> #include <stdlib.h> #include <string> #include <gmp.h> #include <gmpxx.h> #include <time.h> #include <sstream> using namespace std; string metodo_euler(unsigned long int digitos, mp_exp_t &exponente); string metodo_ramanujan(unsigned long int digitos, mp_exp_t &exponente); void imprimir_pi_aux(string pi, mp_exp_t exponente, int digitos); int main(int argc, char **argv) { unsigned long int digitos = strtol(argv[1], NULL, 10); //argv a int mpf_set_default_prec(32 * 10 * (digitos / 100) * 1.11); //precision + 10% long exponente; clock_t start = clock(); string pi; if(argc>2 && argv[2]=="ramanujan"){ pi = metodo_ramanujan(digitos, exponente); }else{ pi = metodo_euler(digitos, exponente); } clock_t end = clock(); imprimir_pi_aux(pi, exponente, digitos); cout << "\ntiempo total de ejecucion: " << (float) (end - start) / CLOCKS_PER_SEC << "\n"; cout << "tiempo total de impresion: " << (float) (clock() - end) / CLOCKS_PER_SEC << "\n\n"; return 0; } void imprimir_pi_aux(string pi, long exponente, int digitos) { cout << "PI: "; stringstream aux; unsigned long int i; if (exponente < 0) { cout << "0."; while (exponente < 0) { cout << 0; exponente++; } } else { for (i = 0; i < exponente; i++) { cout << pi[i]; } cout << ".\n\n1:\t"; } for (i = exponente; i < digitos + 1; i++) { aux << pi[i]; if (i % 10 == 0) aux << ' '; if (i % 500 == 0) aux << endl; if (i % 50 == 0 && i < digitos) aux << endl << i + 1 << ":\t"; } aux << endl; cout << aux.str(); } string metodo_euler(unsigned long int digitos, long &exponente) { digitos /= 100; //trabaja con lotes de 100 unsigned long int precision = digitos * 100 * 3 * 1.12; unsigned long int x, i; mpf_t factorial, sumatoria, buff_factorial; //variables GMP mpf_init_set_ui(factorial, 1); //factorial=1 mpf_init_set_ui(sumatoria, 1); //sumatoria=1 mpf_init_set_ui(buff_factorial, 1); //buff_factorial=1 for (x = 1; x < precision; x++) { i = 2 * x + 1; mpf_set_ui(buff_factorial, x); //buff_factorial=x mpf_div_ui(buff_factorial, buff_factorial, i); //buff_factorial*=i mpf_mul(factorial, factorial, buff_factorial); //factorial*=buff_factorial mpf_add(sumatoria, sumatoria, factorial); //sumatoria+=factorial } mpf_mul_ui(sumatoria, sumatoria, 2); //sumatoria*=2 return mpf_get_str(NULL, &exponente, 10, 0, sumatoria); } string metodo_ramanujan(unsigned long int digitos, long &exponente) { unsigned long int i, j; mpf_t sumatoria, buff_sumatoria, buff_ciclo_superior, buff_ciclo_inferior, primera_parte, buff_ciclo_inferior2, factorial_superior, factorial_inferior; mpf_init_set_ui(sumatoria, 1103); //sumatoria=0 mpf_init_set_ui(buff_sumatoria, 0); //buff_sumatoria=0 mpf_init_set_ui(buff_ciclo_superior, 0); //buff_ciclo_superior=0 mpf_init_set_ui(buff_ciclo_inferior, 0); //buff_ciclo_inferior=0 mpf_init_set_ui(primera_parte, 0); //primera_parte=0 mpf_init_set_ui(buff_ciclo_inferior2, 0); //buff_ciclo_inferior2=0 mpf_init_set_ui(factorial_superior, 1); //factorial_superior=1 mpf_init_set_ui(factorial_inferior, 1); //factorial_inferior=1 mpf_sqrt_ui(primera_parte, 2); //primera_parte=sqrt(2) mpf_mul_ui(primera_parte, primera_parte, 2); //primera_parte*=2 mpf_div_ui(primera_parte, primera_parte, 9801); //primera_parte/=9801 for (i = 1; i <= digitos; i++) { mpf_set_ui(factorial_superior, 1); for (j = 2; j <= i * 4; j++) { mpf_mul_ui(factorial_superior, factorial_superior, j); } mpf_set_ui(buff_ciclo_superior, 26390); mpf_mul_ui(buff_ciclo_superior, buff_ciclo_superior, i); mpf_add_ui(buff_ciclo_superior, buff_ciclo_superior, 1103); mpf_mul(buff_ciclo_superior, buff_ciclo_superior, factorial_superior); mpf_mul_ui(factorial_inferior, factorial_inferior, i); mpf_pow_ui(buff_ciclo_inferior, factorial_inferior, 4); mpf_set_ui(buff_ciclo_inferior2, 396); mpf_pow_ui(buff_ciclo_inferior2, buff_ciclo_inferior2, 4 * i); mpf_mul(buff_ciclo_inferior, buff_ciclo_inferior, buff_ciclo_inferior2); mpf_div(buff_sumatoria, buff_ciclo_superior, buff_ciclo_inferior); mpf_add(sumatoria, sumatoria, buff_sumatoria); } mpf_mul(sumatoria, sumatoria, primera_parte); mpf_ui_div(sumatoria, 1, sumatoria); return mpf_get_str(NULL, &exponente, 10, 0, sumatoria); }
|
|
|
|
« Última modificación: 10 Abril 2014, 04:55 am por engel lex »
|
 En línea
En línea
|
El problema con la sociedad actualmente radica en que todos creen que tienen el derecho de tener una opinión, y que esa opinión sea validada por todos, cuando lo correcto es que todos tengan derecho a una opinión, siempre y cuando esa opinión pueda ser ignorada, cuestionada, e incluso ser sujeta a burla, particularmente cuando no tiene sentido alguno.
|
|
|
do-while
 Desconectado Desconectado
Mensajes: 1.276
¿Habra que sacarla de paseo?

|
¡Buenas! Te ha faltado calcular el factorial inferior: Tu código: mpf_mul_ui(factorial_inferior, factorial_inferior, i); //linea 104 mpf_pow_ui(buff_ciclo_inferior, factorial_inferior, 4);
Corregido: mpf_set_ui(factorial_inferior, 1); for (j = 2; j <= i ; j++) { mpf_mul_ui(factorial_inferior, factorial_inferior, j); } mpf_pow_ui(buff_ciclo_inferior, factorial_inferior, 4);
Creo que eso era todo. ¡Saludos! |
|
|
|
|
 En línea
En línea
|
- Doctor, confundo los números y los colores.
- Vaya marrón.
- ¿Marrón? ¡Por el culo te la hinco!
|
|
|
|
engel lex
|
no, el factorial inferior si se calcula, lo hago igual que el de euler, es decir como es un factorial que crece de 1 en 1 uso el ciclo principal para evitar hacer más ciclos
fíjate que el factorial superior inicia reasignándose y el inferior no... pero me diste una idea para hacer algo similar con el superior
|
|
|
|
|
 En línea
En línea
|
El problema con la sociedad actualmente radica en que todos creen que tienen el derecho de tener una opinión, y que esa opinión sea validada por todos, cuando lo correcto es que todos tengan derecho a una opinión, siempre y cuando esa opinión pueda ser ignorada, cuestionada, e incluso ser sujeta a burla, particularmente cuando no tiene sentido alguno.
|
|
|
do-while
 Desconectado Desconectado
Mensajes: 1.276
¿Habra que sacarla de paseo?

|
no, el factorial inferior si se calcula, lo hago igual que el de euler, es decir como es un factorial que crece de 1 en 1 uso el ciclo principal para evitar hacer más ciclos
El factorial inferior lo tienes que recalcular en cada iteracion. No es el factorial de n, siendo n el numero de iteraciones. Para cada iteración k es el factorial de k. Si dices que no te da el resultado, en algún punto tiene que haber un error. ¿No? Además, de la forma en la que lo haces no estas calculando el factorial de nada. Estas multiplicando un acumulador por el numero de ciclo y luego lo elevas a 4, lo multiplicas por el siguiente contador de ciclo y lo vuelves a elevar a 4. Eso no es lo que indica la fórmula...
|
|
|
|
« Última modificación: 10 Abril 2014, 14:47 pm por do-while »
|
 En línea
En línea
|
- Doctor, confundo los números y los colores.
- Vaya marrón.
- ¿Marrón? ¡Por el culo te la hinco!
|
|
|
|
engel lex
|
mira como lo hice en euler  si tengo un error, pero hice ya el debug porque justamente se que esa es la principal posible primera falla  factorial_inferior = 1 // 0! ciclo 1: factorial_inferior *=1 //1*1 = 1 ciclo 2: factorial_inferior *=2 //2*1*1 = 2 ciclo 3: factorial_inferior *=3 //3*2*1*1 = 6 ciclo 4: factorial_inferior *=4 //4*3*2*1*1 = 24 ciclo 5: factorial_inferior *=5 //5*4*3*2*1*1 = 120 el arrastra el valor del factorial y lo multiplica cada vez, por eso no le reasigno un valor entero  (así evito hacer un ciclo extra con una variable de 1kb o más) el superior lo voy a hacer similar corriéndolo solo de i*4 y x< (i+1)*4 así solo hace 4 ciclos por ciclo  pero esa parte si está funcionando... comprobado (hace 15 segundos XD) sospecho que tendré que hacer debug con buena calma ver los valores con lápiz en mano... porque en donde sospecho que puede salir el error es en uno de esos números grandes |
|
|
|
« Última modificación: 10 Abril 2014, 15:24 pm por engel lex »
|
 En línea
En línea
|
El problema con la sociedad actualmente radica en que todos creen que tienen el derecho de tener una opinión, y que esa opinión sea validada por todos, cuando lo correcto es que todos tengan derecho a una opinión, siempre y cuando esa opinión pueda ser ignorada, cuestionada, e incluso ser sujeta a burla, particularmente cuando no tiene sentido alguno.
|
|
|
Gh057
 Desconectado Desconectado
Mensajes: 1.190

|
buenas! entré un segundo justo antes de ir a dormir, ando complicado con los tiempos jejej y recién veo el tema! pero no quería dejar el sitio sin antes felicitarte engel lx por el post, es muy interesante! tan solo a titulo informativo, el excelente algoritmo de Ramanujan ha sido modificado ligeramente obteniéndose el algoritmo de Chudnovsky, que permite algo así como 15 decimales de exactitud creo, luego de cada término XD una locura! 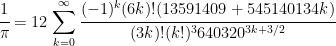 pd: acabo de buscarlo, son 14 decimales; de 9 que se obtenía con el anterior. tengo entendido que los últimos records que indicaban más arriba fueron con dicha implementación. saludos |
|
|
|
|
 En línea
En línea
|
4 d0nd3 1r4 3l gh057? l4 r3d 3s 74n v4s74 3 1nf1n1t4...
|
|
|
|
engel lex
|
do-while: lo que es la arrogancia! XD al final si era el factorial el error! XD (eso creo) XD pero ahorita está más feo aún pero funciona! y es increiblemente eficiente! de ahora en adelante publicaré el codigo en el post inicial... no lo publicaré como un gran bloque sino, cada sección... olvidense de imprimir en archivo y de la modularidad! XD eso aún lo postergo Gh057: lo había visto! XD pero me tomará otro dia adaptarlo, aunque como tiene similaridad con Ramanujan no se me debría ser tan difícil... alguna vez vi algo de comentario de código cómicos... este merece uno que vi //cuando empeze a hacer esto solo dios y yo sabiamos lo que hacia, en este momento solo dios lo sabe
aqui la correccion de Ramanujan string metodo_ramanujan(unsigned long int digitos, long &exponente) { digitos/=8; digitos*=1.01; unsigned long int i, j; mpf_t sumatoria, buff_sumatoria, buff_ciclo_superior, buff_ciclo_inferior, primera_parte, buff_ciclo_inferior2, factorial_superior, factorial_inferior; mpf_init_set_ui(sumatoria, 1103); //sumatoria=0 mpf_init_set_ui(buff_sumatoria, 0); //buff_sumatoria=0 mpf_init_set_ui(buff_ciclo_superior, 0); //buff_ciclo_superior=0 mpf_init_set_ui(buff_ciclo_inferior, 0); //buff_ciclo_inferior=0 mpf_init_set_ui(primera_parte, 0); //primera_parte=0 mpf_init_set_ui(buff_ciclo_inferior2, 0); //buff_ciclo_inferior2=0 mpf_init_set_ui(factorial_superior, 1); //factorial_superior=1 mpf_init_set_ui(factorial_inferior, 1); //factorial_inferior=1 mpf_sqrt_ui(primera_parte, 2); //primera_parte=sqrt(2) mpf_mul_ui(primera_parte, primera_parte, 2); //primera_parte*=2 mpf_div_ui(primera_parte, primera_parte, 9801); //primera_parte/=9801 for (i = 1; i <= digitos; i++) { for (j = (i - 1)*4 + 1; j <= i * 4; j++) { mpf_mul_ui(factorial_superior, factorial_superior, j); } mpf_set_ui(buff_ciclo_superior, 26390); mpf_mul_ui(buff_ciclo_superior, buff_ciclo_superior, i); mpf_add_ui(buff_ciclo_superior, buff_ciclo_superior, 1103); mpf_mul(buff_ciclo_superior, buff_ciclo_superior, factorial_superior); mpf_mul_ui(factorial_inferior, factorial_inferior, i); mpf_pow_ui(buff_ciclo_inferior, factorial_inferior, 4); mpf_set_ui(buff_ciclo_inferior2, 396); mpf_pow_ui(buff_ciclo_inferior2, buff_ciclo_inferior2, 4 * i); mpf_mul(buff_ciclo_inferior, buff_ciclo_inferior, buff_ciclo_inferior2); mpf_div(buff_sumatoria, buff_ciclo_superior, buff_ciclo_inferior); mpf_add(sumatoria, sumatoria, buff_sumatoria); } mpf_mul(sumatoria, sumatoria, primera_parte); mpf_ui_div(sumatoria, 1, sumatoria); return mpf_get_str(NULL, &exponente, 10, 0, sumatoria); }
si no fuera tan flojo (y estuviera claro en el tema), intentara hacer operator overload para usar los operadores normales! D: a partir de ahora modifico el post principal |
|
|
|
« Última modificación: 11 Abril 2014, 08:17 am por engel lex »
|
 En línea
En línea
|
El problema con la sociedad actualmente radica en que todos creen que tienen el derecho de tener una opinión, y que esa opinión sea validada por todos, cuando lo correcto es que todos tengan derecho a una opinión, siempre y cuando esa opinión pueda ser ignorada, cuestionada, e incluso ser sujeta a burla, particularmente cuando no tiene sentido alguno.
|
|
|
|
| Mensajes similares |
|
Asunto |
Iniciado por |
Respuestas |
Vistas |
Último mensaje |

|

|
Bitrate + Motion Search Precision
Multimedia
|
G3N3S1S
|
2
|
2,852
|
 13 Enero 2005, 23:23 pm
13 Enero 2005, 23:23 pm
por fanny
|

|

|
pequeño aporte(proxy),pero aporte al fin.:D
Programación Visual Basic
|
Tengu
|
0
|
3,142
|
 22 Julio 2007, 17:33 pm
22 Julio 2007, 17:33 pm
por Tengu
|

|

|
Obtener más precisión que long double en C?¿?
Programación C/C++
|
jhonsc
|
3
|
3,883
|
 4 Febrero 2012, 13:48 pm
4 Febrero 2012, 13:48 pm
por Xandrete
|

|

|
Problema con la precisión del double
Java
|
danielo-
|
4
|
5,807
|
 27 Marzo 2012, 21:07 pm
27 Marzo 2012, 21:07 pm
por danielo-
|

|

|
Prueban en Atapuerca una tecnología inalámbrica de alta precisión pionera en...
Noticias
|
wolfbcn
|
0
|
1,674
|
 27 Junio 2012, 21:21 pm
27 Junio 2012, 21:21 pm
por wolfbcn
|
 |





 Autor
Autor



 En línea
En línea



 vamos con esa! voy a extender el programa... ya llegué a mi casa, tengo 1,5l de te negro listos y 250g de maní japonés! ese código sale en un rato!
vamos con esa! voy a extender el programa... ya llegué a mi casa, tengo 1,5l de te negro listos y 250g de maní japonés! ese código sale en un rato!