teoricamente debe ser como una cebolla según como funcione tikvpn (lo desconozco), si es a nivel de adaptador, será el "mas externo"



la conexión va algo como




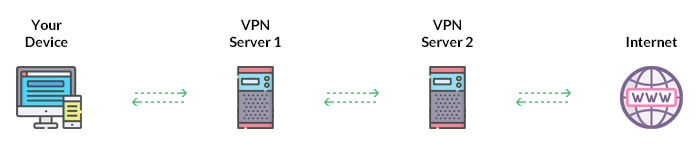
donde tu pc abre un tinel que va al servidor de tikvpn, de allí tu opera abre un tunel que pasa por tikvpn y llega hasta el sercidor de vpn de opera, desde ese ultimo al internet

basicamente tikvpn sería Server1 y opera vpn sería Server2

es decir, tik sabe quien eres, pero no que data estás enviando, sabe nada más que vas a opera, por otro lado, opera no sabe quien eres pero sabe la data y a donde vas

aclaremos algo, virtualmente es posible, pero hacerlo en batch es como hacer una bicicleta con ruedas cuadradas.... bqtch no es un lenguaje de programación, es un lenguaje de manejo de archivos por lotes

si   una total locura de precios... si lo comparamos en plan con OVH

https://www.ovhcloud.com/es/vps/

5$ al mes por 1 nucleo, 2gb de ram, 40gb de disco y red de 250mbps

ese servicio son em promedio 15$ al mes, por 0.5gb de ram, 20gb de disco, 100mbps de red, y nucleos solo dios sabe  

ni anonimous, ni tormenta solares, un lio enel registro dns, ya hace un par de meses habia pasado con otros sevicios cuando una empresa actualizando servidores tuvo una caida

exacto, si el isp ve que un paquete va a esa direccion, solo lo redirige y listo... por eso necesitas algo como una vpn para llegar hasta otra red donde el isp no te desvie y salir desde alli


por cierto, entrando desdemi ubicacion (Caracas) me muestra que la pagina esta bloqueada por el gobierno de españa...

es decir, no es un lio de isp... es simplemente que esa ip esta apuntando a algun servidor del gobierno que muestra ese mensaje...

no hay nada que puedas hacer con o sin vpn... ese servidor esta muerto

tal cual lo dice RayR

"flashear" es solo un nombre para copiar archivos a la memoria del dispositivo...  es mas  parecido a actualizar una bios que formatear un windows

entrar a un  ip bloqueada por el gobierno sin usar medios que te pongan fuera del pais no funciona...

necesitas proxy, vpn o algo similar porque si...

solo lo he hecho dentro de parametros para cambiar el bootloader y el os de fabrica de una tablet... ojo tanto elbootloader que estaba metiendo como el os, eran diseñados para el mismo equipo, siempre te  advierten que si metes el equivocado (asi sea de la versin "A" a la "B" matas el  equipo)

adb.... solo necesitas buscar en google y te recomiendo para que leas que es y como funciona

mi recomendacion es que agarres un equipo popular (y que estés dispuesto a sacrificar) y busques "custom rom" (OS personalizados) y practiques con eso para que tengas una idea de los segmentos involucrados

claro, siempre es mejor eso...pero el infectarse no esta  en control de uno... te aseguro que yo no lo escogi y literalmente cruzo la puerta de mi casa 2 veces por semana con todas las respectivas medidas

no es tan simple ya que el dispositio no esta diseñado para ser asi de abierto

sin embargo por adb puedes acceder a las diferentes secciones de memoria, esto puede variar de un dispositivo a otro, y como depende del bootloader del telefono el encargarse de dichos accesos, si dañas el bootloader o la estructura del disco, quedará irrecuperable el equipo (a menos que sepas escribir la memoria interna por vias de terceros)

imagina que tu pc tiene la bios y el OS en el disco y dañas la  bios...

sobre el OS tampoco sera tan simple como un windows en x86, esto debido a que los telefonos varian mas en hardware y no hay unos estandares mayores a segir , asi que cada OS tiene que estar modificado para adaptarse a dicho hardware