¡Buenas!
Creo que lo mas intuitivo es trabajar con la funcion inversa y aplicar Bolzano:
x = loga(b) -> ax = b -> ax - b = 0
Por lo tanto se trata de encontrar el cero de la función f(x) = ax - b
Aplicando un poco de analisis sabemos que ax es siempre positivo (siempre que a sea positivo), por lo tanto tal cero existirá si y solo si b es positivo.
En estas condiciones tendrás que buscar dos puntos x0 y0 en los que la función tenga signo distinto. Así sabrás que el cero de la función se encuentra entre estos dos puntos.
Solo te queda iterar. En cada paso tendrás que buscar el punto medio del intervalo y evaluarlo para saber si la función toma un valor positivo o negativo en dicho punto. Una vez sepas el valor de la función al evaluarlo en el punto medio podrás sustituir la cota superior o inferior que tenias inicialmente por el punto medio.
Este proceso parará cuando:
- La evaluación de la función en el punto medio de exactamente cero.
- La diferencia entre la cota superior e inferior sea menor a un valor que tu consideres un error aceptable para la solución del problema.
- Cuando entre una iteración y la siguiente no cambie el punto medio (esto sucede debido al incremento mínimo que existe en la representación interna de números en coma flotante)
El valor que devolverá la función logaritmo será el punto medio del intervalo en el que han acabado las iteraciones, ya que será el valor de x que ha hecho que la función f(x) = ax - b se aproxime mas a cero (el valor mas proximo a loga(b))
¡Saludos!

|
 |
Bienvenido(a), Visitante. Por favor Ingresar o Registrarse ¿Perdiste tu email de activación?. |



 Autor
Autor



 En línea
En línea




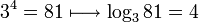

 ). En cuanto lo último comentado por @Puntoinfinito eso solo vale para logaritmos exactos. ¿@do-while al fin y al cabo es ensayo y error no? Si yo tengo log24 -> 2x = 4 vas probando valores enteros hasta que tengas un resultado mayor que 4 o igual y vas reduciendo ... no sé tampoco tengo nivel matemático para hacerlo, implemente la serie de Taylor pero es muy lenta, dejo el código al que @diskontrol se refería:
). En cuanto lo último comentado por @Puntoinfinito eso solo vale para logaritmos exactos. ¿@do-while al fin y al cabo es ensayo y error no? Si yo tengo log24 -> 2x = 4 vas probando valores enteros hasta que tengas un resultado mayor que 4 o igual y vas reduciendo ... no sé tampoco tengo nivel matemático para hacerlo, implemente la serie de Taylor pero es muy lenta, dejo el código al que @diskontrol se refería:




