 Autor Autor
|
Tema: Variaciones de La Quiniela y números en base 3 (Leído 9,668 veces)
|
okik
 Desconectado Desconectado
Mensajes: 462

|
Buenas Para los que no lo sepan La Quiniela es un juego de azar, un sistema de apuestas popular en España, basada en la liga española de fútbol y gestionado por Loterías y Apuestas del Estado
(LAE) Dicho juego consiste en una columna de catorce apuestas correspondiente a catorce partidos de fútbol, normalmente de primera y segunda división, pero a falta de ellos por calendario pueden usarse partidos de otros campeonatos importantes, incluso de selecciones. El objetivo es acertar [1] Gana el equipo que juega en casa, [X]Empate, [2] Gana el equipo que juega fuera de casa. Se añade ademas una quinceaba apuesta basada en el número de goles de un partido 0 1 2 M Donde M son más de 2 goles.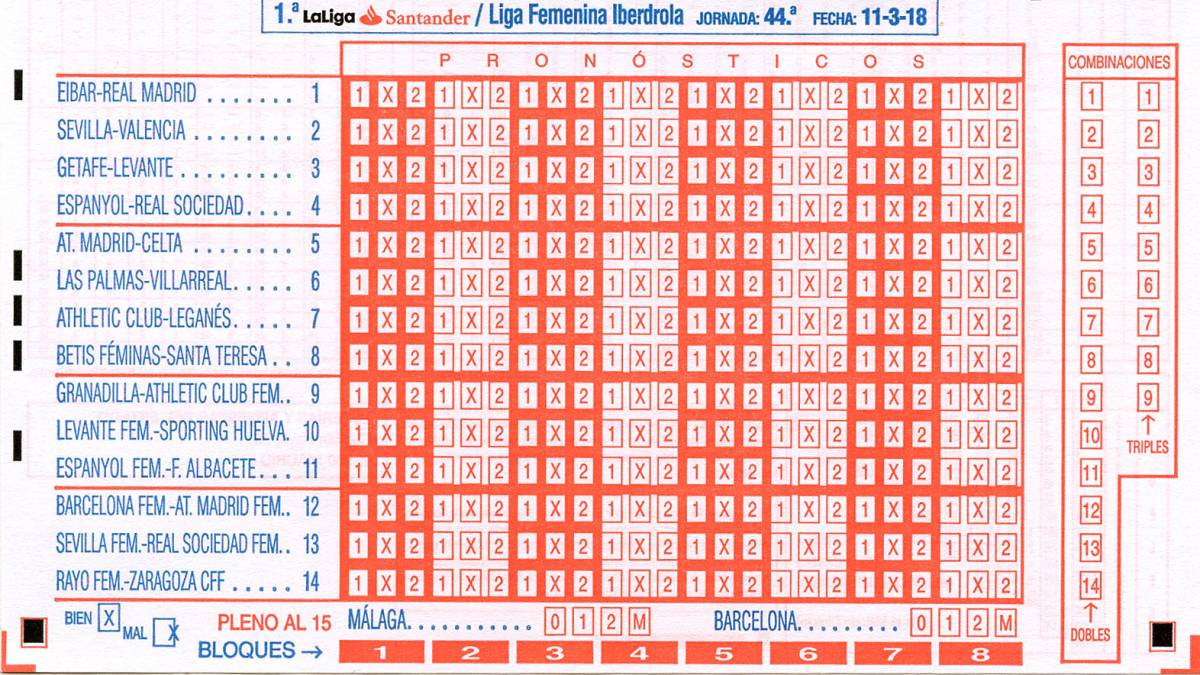 ¿Qué tiene esto que ver con los números en base 3? ¿Qué tiene esto que ver con los números en base 3?A ver, esto no es algo que acabe de descubrir pero hace tiempo que no publico nada aquí y se me ha ocurrido que era una curiosidad interesante a publicar en este foro. De hecho es algo que usé en un trabajo de investigación del Bachillerato por el 2015 sobre juegos de azar. Pero lo sabía desde el 2004 más o menos, cuando investigué para realizar un programa de ordenador sobre este juego (sin Internet), matizo esto porque hoy en día se puede encontrar casi cualquier cosa sobre este juego en Internet. Sin embargo sobre esto no he encontrado nada de nada y ya es difícil. ¿Nadie ha visto la relación? Quizás no he buscado bien, en fin no sé, pero por esta razón he decidido publicar esto. Pues bien, resulta que las variaciones que resultan de rellenar una columna de catorce apuestas de La Quiniela pueden convertirse o interpretarse como números en base 3. Si escribimos una columna cualquiera linealmente nos sale algo así: 1X1212121111XXExiste una fórmula muy simple para saber el número de variaciones que se pueden realizar, llamadas Variaciones con repetición. Consiste en una potencia cuya base es el número de signos o elementos, [1X2] en este caso que serían tres y lo elevamos al número de elementos que combinamos que serían catorce. Finalmente obtenemos: 3^14= 4782969 variaciones.Luego podríamos pasarnos todo el día haciendo variaciones hasta que nos cansáramos. Pero, ¿Cómo puedo hacer variaciones en orden, desde 11111111111111, a 222222222222222 sin repetir una sola hasta obtener las 4782969 posibles? Esta es la pregunta que me hice cuando quise realizar un programa que fuera capaz de realizar todas las variaciones en orden correlativo. Es más, poder obtener cual sería la variación 3512 por ejemplo o la número 3125245. La solución que encontré fue convertirlos o interpretarlos como números en base 3. Para ello basta con sustituir el 1 por 0, la X por 1, y el 2 lo dejamos como está. Por ejemplo, la variación que puse más arriba sería 01020202000011: Variación de La Quiniela
1X1212121111XXMisma variación interpretada como número en Base 3
01020202000011¿Qué orden ocupa?Solo hay que pasarlo a un número decimal para obtener su lugar dentro de las 4782969 variaciones. Igualmente se puede hacer a la inversa. Pasar un número decimal a base tres y luego obtener la variación de la quiniela. Para el proceso de conversión de cualquier base hay vídeos por ahí de binario a decimal pero usan tablas y lo ponen como más complicado de lo que és. El proceso es realmente muy simple, consiste en coger el primer dígito multiplicarlo por la base elevada a la posición que ocupa el dígito empezando por la derecha y desde 0. 2121110= 0·3^0 + 1·3^1 + 1·3^2 + 1·3^3 + 2·3^4 + 1·3^5 + 2·3^6 = 1902
Lo pondré entre corchetes para que se vea más claro donde b es igual a la base 2121110= [0 * b^0] + [1 * b^1] + [1 * b^2] + [1 * b^3] + [2 * b^4] + [1 * b^5] + [2 * b^6] = 1902
Así para saber que lugar ocupa cualquier variación que hagamos de La Quiniela tan solo hay que convertirlo en un número de base tres y luego realizar la operación de conversión a decimal y sumarle uno al resultado. Hacerlo manualmente o con calculadora resulta tedioso, sin embargo se puede hacer con un simple código. El algoritmo para convertir un número en base 3 a decimal con C# es bien simple (por lo menos el que he hecho yo, es lo que creo): string strNumB3 = "0"; //Numero en base 3 int RepLoop = strNumB3.Length; //segun el numero de digitos repeticiones para el bucle int NumDec = 0; for (int I = RepLoop - 1; I >= 0; I--) { NumDec += Convert.ToInt32(strNumB3.Substring(I, 1)) * (int)(Math.Pow(3, RepLoop - I - 1)); } NumDec += 1; Console.WriteLine(NumDec); Console.ReadLine();
En este caso devuleve 1 porque he establecido a numB3 el valor 0. Como expliqué arriba el 1 equivale a 0 La primera variación es 11111111111111 = 00000000000000 = 0 = 0
La segunda variación es 111111111111X = 00000000000001 = 1 = 1
La tercera variación es 1111111111112= 00000000000002 = 2 = 2
La cuarta variación es 111111111111X1=00000000000010= 10 = 3
La quinta ariación es 111111111111XX=00000000000011= 11 = 4
La sexta ariación es 111111111111X2=00000000000012= 12 = 5
Si se observa bien he añadido un 1 al resultado del algoritmo en la línea 8: Esto es porque el número cero en base tres es obviamente cero, y no tiene sentido decir la variación número cero, de modo que le sumo un uno para determinar el orden correcto ya que la primera 11111111111111 cuyo "equivalente" en base tres sería 0000000000000 sería 1 y finalmente 22222222222222 será 4782969, como puede comprobarse tras ejecutar el siguiente código: using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace ConsoleApplication1 { class Program { static void Main(string[] args) { string Quiniela = "22222222222222".Replace("1", "0").Replace("X", "1").Replace("x", "1"); string strNumB3 = Quiniela; //Numero en base 3 int RepLoop = strNumB3.Length; //segun el numero de digitos repeticiones para el bucle int NumDec = 0; for (int I = RepLoop - 1; I >= 0; I--) { NumDec += Convert.ToInt32(strNumB3.Substring(I, 1)) * (int)(Math.Pow(3, RepLoop - I - 1)); } NumDec += 1; Console.WriteLine(string.Format("{0} es la variacion numero {1}",Quiniela , NumDec)); Console.ReadLine(); } } }
Esto lo tenía en VB6 ya que cuando lo desarrollé usaba esa programación y lo he actualizado a C#. Menudo cambio ¿no? '... F = Mid(strA, 14, 1) + Mid(strA, 13, 1) * 3 + Mid(strA, 12, 1) * 3 ^ 2 + Mid(strA, 11, 1) * 3 ^ 3 + Mid(strA, 10, 1) * 3 ^ 4 + Mid (strA, 9, 1) * 3 ^ 5 + Mid(strA, 8, 1) * 3 ^ 6 + Mid(strA, 7, 1) * 3 ^ 7 + Mid(strA, 6, 1) * 3 ^ 8 _ + Mid(strA, 5, 1) * 3 ^ 9 + Mid(strA, 4, 1) * 3 ^ 10 + Mid(strA, 3, 1) * 3 ^ 11 + Mid(strA, 2, 1) * 3 ^ 12 '...
Quizás encontréis una forma más eficiente de calcularlo de la que yo he usado en C#. El proceso inverso, es decir pasar de decimal a base 3 podría ser este: int NumB10 = 1; //Numero basado en el total de variaciones (3^14) de La Quiniela string numB3 = string.Empty; //Variable para el numero en Base 3 NumB10 -= 1; //Le resto 1 al numero en base 10 do { numB3 = NumB10 % 3 + numB3; NumB10 = NumB10 / 3; } while (NumB10 > 0); Console.WriteLine(numB3); Console.ReadLine();
Se basa en un algoritmo matemático bastante sencillo que se puede realizar en papel con bolígrafo en mano. Modificando un poco el código en C# que he puesto se puede hacer para cualquier tipo de conversión pero el que he puesto arriba es sólo de número en base 10 a base 3. Nótese que inicialmente resto 1 al número en base 10, esto es porque como expliqué más arriba la primera variación equivale 0 en base 3; 11111111111111= 00000000000000= 0.
Volviendo al objetivo que era poder escribir las variaciones en orden correlativo aquí dejo un sencillo código en el que se puede realizar una serie de variaciones en orden correlativo desde A a B, (NOTA: La consola sólo puede mostrar un número total de 299 líneas, por lo que si se generan más de 299 variaciones solo se verán las 299 últimas). using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace ConsoleApplication1 { class Program { static void Main(string[] args) { int min = 1; int max = 299; for (int n = min - 1; n < max; n++) { string B3 = string.Format("{0:00000000000000}", Convert.ToInt64(ConvNumB3(n))); string Variacion = B3.Replace("1", "X").Replace("0", "1"); Console.WriteLine(string.Format("{0}= {1}= {2}", n + 1, B3, Variacion)); } Console.ReadLine(); } static string ConvNumB3(int NumB10) { string numB3 = string.Empty; do { numB3 = NumB10 % 3 + numB3; NumB10 = NumB10 / 3; } while (NumB10 > 0); return numB3; } } }
 Quizás haya otra manera para poder crear las variaciones en orden ¿Quizás con LINQ? mmm se me escapa. En cualquier caso la interpretación de números en base 3 y las variaciones de la quiniela existe, así como la forma de establecer una posición, un orden para cada variación. Saludos.
|
|
|
|
« Última modificación: 28 Mayo 2018, 01:58 am por okik »
|
 En línea
En línea
|
|
|
|
|
|
okik
 Desconectado Desconectado
Mensajes: 462

|
Hola NEBIRE Gracias por el aporte, hoy no tengo tiempo de analizarlo con detalle, pero seguro que me resulta de utilidad. El objetivo del ejercicio no es combinar, ya que eso es algo relativamente fácil. Sino que se trata de obtener o saber qué posición ocupa X variación o combinación de elementos dentro de un orden lógico. La gracia está en que se puede realizar con cualquier tipo de combinatoria, ya sean objetos, letras, signos, lo que sea. Simplemente convirtiendo la combinación de elementos en números cuya base dependerá del número de elementos. Como en este caso, en La Quiniela, solo hay tres [1X2] la base es 3.
|
|
|
|
« Última modificación: 28 Mayo 2018, 13:54 pm por okik »
|
 En línea
En línea
|
|
|
|
|
|
okik
 Desconectado Desconectado
Mensajes: 462

|
Podrías ser más específico y no poner equilicuá, un enlace y ya está. Así a ojo viendo el enlace no veo que puedas saber por ejemplo qué lugar ocupa esta variación: XXXX12111222XX Sin haber generado ni una sola variación. No vale por ejemplo crear X variaciones o combinaciones que están en una matriz o en memoria o crear un bucle y establecer una condición y decir, vale esta variación y está en tal lugar. Muéstrame un sistema diferente al mío donde puedas obtener el orden que ocupa dentro de un orden lógico único de menor a mayor (ya que solo hay uno para cada tipo) sin bucles, sin generar variaciones. Tal como así: De 2X2XXX1 a 2121110 y después 2121110= 0·3^0 + 1·3^1 + 1·3^2 + 1·3^3 + 2·3^4 + 1·3^5 + 2·3^6 = 1902 (+1) ya lo tienes. Se puede hacer sin ni siquiera un ordenador o programa, simplemente con bolígrafo y papel como he explicado más arriba. Este código de abajo lo puse no como muestra de como generar las variaciones sino para que se pueda visualizar el orden lógico correcto de cada variación y la posición que ocupa dentro de este orden. Este código: using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace ConsoleApplication1 { class Program { static void Main(string[] args) { int min = 1; int max = 299; for (int n = min - 1; n < max; n++) { string B3 = string.Format("{0:00000000000000}", Convert.ToInt64(ConvNumB3(n))); string Variacion = B3.Replace("1", "X").Replace("0", "1"); Console.WriteLine(string.Format("{0}= {1}= {2}", n + 1, B3, Variacion)); } Console.ReadLine(); } static string ConvNumB3(int NumB10) { string numB3 = string.Empty; do { numB3 = NumB10 % 3 + numB3; NumB10 = NumB10 / 3; } while (NumB10 > 0); return numB3; } } }
Repito por tema de trabajo no tengo tiempo de mirarme con detenimiento los enlaces pero seguro aprendo algo o incluso ese "equilicua" tenga sentido. De nuevo gracias
|
|
|
|
« Última modificación: 29 Mayo 2018, 02:22 am por okik »
|
 En línea
En línea
|
|
|
|
|
Serapis
|
elimino, el mensaje salió duplicado, al tratar de modificarlo... cosa de los deslogeos...
|
|
|
|
« Última modificación: 29 Mayo 2018, 18:00 pm por NEBIRE »
|
 En línea
En línea
|
|
|
|
|
Serapis
|
Podrías ser más específico y no poner equilicuá, un enlace y ya está. http://dle.rae.es/?id=FznyqURAsí a ojo viendo el enlace no veo que puedas saber por ejemplo qué lugar ocupa esta variación:
XXXX12111222XX
Sin haber generado ni una sola variación. No vale por ejemplo crear X variaciones o combinaciones que están en una matriz o en memoria o crear un bucle y establecer una condición y decir, vale esta variación y está en tal lugar. Está todo allí, bastante claro, si te tomas la molestia de leerlo... entresaco un par de párrafos que inicialmente resumen bastante. vamos con el primero, el algoritmo-A.
El algoritmo-A, es el más simple de todos en cuanto a líneas de código y como dije es solo un cambio de base de numeración a la base cuyo tamaño representa el alfabeto usado. Es el algoritmo al que todo el mundo (que sepa un mínimo de programación debiera llegar...
- Su fuerte, la extrema sencillez de entenderlo... (y programarlo).
- Su defecto, que no es el más óptimo en cuanto a velocidad.
...
El conjunto de caracteres puede optarse por todo el ASCII (o una parte definiendo un punto de inicio y una cantidad de caracteres), o restringido a los caracteres: 0-9, A-Z, a-z, o cualquier combinación de ellas (pero siempre en el orden en que aparecen. También permite recibir un alfabeto personalizado (básicamente un array con los caracteres que se desee y en el orden que se quiera). Para el propósito de este texto es suficiente ... (una interfaz sencilla basada en A-Z, 0-9, etc..) En el primer pedazo de código se definen funcionalidad previa, enumeraciones y tal, como se indica aquí: ... - Luego hay 4 constructores de clase, para permitir invocar el tipo de alfabeto de que se quiere generar en base a las opciones que permite. (para ! X " habría que elegir Custom, y pasar la cadena ("1X2") - Finalmente hay un método que construye el alfabeto. La idea de esta clase, es que el alfabeto sea definido una sola vez y pueda ser usada como parámetro para enumerar. Así se evita que mientras se enumere se modifique el alfabeto (o el tamaño del mismo) y dé lugar a errores durante la ejecución. Ya que se construye y luego es de solo lectura, no puede modificarse mientras se usa. El siguiente código, copiado de allí: El bucle interno que realiza toda la operatoria, para generar una permutación y el bucle externo para iterar entre ttodas las permutaciones. Do v = k n = Numchars Do x = (v Mod p_Sizealfabeto) Clave(n) = p_Alfabeto(x) ' convertir el byte a char. v \= p_Sizealfabeto ' división entera. n -= 2 Loop While (n >= 0) ' USAR la clave desde aquí ' llamada a FuncionX(Clave) k += 1 Loop While (k < s_MaxPermutaciones)
Muéstrame un sistema diferente al mío donde puedas obtener el orden que ocupa dentro de un orden lógico único de menor a mayor (ya que solo hay uno para cada tipo) sin bucles, sin generar variaciones. Tal como así: De 2X2XXX1 a 2121110 y después 2121110= 0·3^0 + 1·3^1 + 1·3^2 + 1·3^3 + 2·3^4 + 1·3^5 + 2·3^6 = 1902 (+1) ya lo tienes. Equilicuá... si ya has visitado el enlace para saber lo que significa, tu pregunta sobra... Justo las líneas antes del bucle, señalé esto: If (.PermutacionInicialLng < 0) Then .PermutacionInicialLng = 0 If (.PermutacionInicialStr.Length > 0) Then ' FALTA: código para convertir la clave a la enésima permutación. ' es el proceso inverso al seguido en el algoritmo y debiera facilitarse como una función pública. ' k= EnesimaPermutacion(.PermutacionStr) ' La función que devolvería el índice de la permutación reclamada. Else k = .PermutacionInicialLng End If
Convertir una clave-apuesta (permutación) a un número indexado de permutación dentro de todas las permutaciones, es (como señalo en dicho texto) la operación inversa... Resulta tan obvio, que ni me molesté en hacerlo. En general con ese algoritmo (el primero de 4), la única forma de parar en una permutación específica para poder continuar desde donde se dejó en otro momento, exije precisamente convertir una permutación a su valor numérico (el enésimo en la permutación, justamente para luego sumar 1 y seguir generando permutaciones partiendo de ese valor)... Más arriba al comentar sobre ese algoritmo, describiía que es el más sencillo, pero también el más lento de los 4. Todas las permutaciones de la quiniela (3^14= 4'7millones), en éste equipo desde el que escribo, que data del 2008, las genera en 3'99 segundos, en tanto los otros algoritmos, los generan 2-3 órdenes más rápidos (cientos-miles de veces más rápido)... no se requieren multiplicaciones, divisiones, módulo... solo suma 1 para un único carácter (de toda la palabra) para generar la siguiente permutación. En los otros no puedo computar el tiempo exacto, siempre da 0 TICKS (frente a los casi 40millones de ticks). En definitiva, lo que te decía al principio es que esto es pura combinatoria, tratarlo como algo distinto, aleja el sentido matemático de un problema conocido, hacia algo que pueda parecer 'raro'... generar claves = generar las apuestas de la quiniela. Es lo mismo, solo cambia el alfabeto usado ("1X2", para la quiniela) y el tamaño de 'palabras' a generar (para la quiniela una palabra de 14 caracteres). Cambiando el nombre porque el dominio social sea diferente, no lo convierte en ningún problema nuevo ni distinto, de ahí que cuando señalaste que no habías encontrado 'fuentes', sin estar errado, no llega a ser cierto... es solo porque has buscado por un nombre específico, en vez del genérico del problema.
Si quieres hacer algo interesante sobre las quinielas (y de lo que no hay apenas literatura), te comento por ejemplo que intentes lograr cuántas y cuáles permutaciones para 4 partidos, son las mínimas necesarias para asegurar siempre que se aciertan al menos 3 (de los 4 partidos). Es decir que jugando x apuestas para 4 partidos, tengas asegurado (al menos) 3 aciertos... y cuáles son, o mejor dicho, como obtener las combinaciones de dichas apuestas... teniendo en cuanta que todas las permutaciones posibles para esas 4partidos, son al menos 3 triples (27 apuestas) y un partido fijo en las 27 apuestas, que lógicamente son costosas (los triples), ¿...se puede asegurar 3 aciertos con menos apuestas que las 27?... Esto es algo conocido, aunque te comento que existen muchas combinaciones (y curiosamente la ONLAE, solo contempla 1), más aún esto se puede ampliar a 5, 6, 7, etc... partidos, que lo hace todavía más interesante... Saludos.
|
|
|
|
« Última modificación: 29 Mayo 2018, 04:32 am por NEBIRE »
|
 En línea
En línea
|
|
|
|
okik
 Desconectado Desconectado
Mensajes: 462

|
http://dle.rae.es/?id=FznyqUREstá todo allí, bastante claro, si te tomas la molestia de leerlo... entresaco un par de párrafos que inicialmente resumen bastante.En el primer pedazo de código se definen funcionalidad previa, enumeraciones y tal, como se indica aquí: ... - Luego hay 4 constructores de clase, para permitir invocar el tipo de alfabeto de que se quiere generar en base a las opciones que permite. (para ! X " habría que elegir Custom, y pasar la cadena ("1X2") - Finalmente hay un método que construye el alfabeto. La idea de esta clase, es que el alfabeto sea definido una sola vez y pueda ser usada como parámetro para enumerar. Así se evita que mientras se enumere se modifique el alfabeto (o el tamaño del mismo) y dé lugar a errores durante la ejecución. Ya que se construye y luego es de solo lectura, no puede modificarse mientras se usa. El siguiente código, copiado de allí: El bucle interno que realiza toda la operatoria, para generar una permutación y el bucle externo para iterar entre ttodas las permutaciones. Do v = k n = Numchars Do x = (v Mod p_Sizealfabeto) Clave(n) = p_Alfabeto(x) ' convertir el byte a char. v \= p_Sizealfabeto ' división entera. n -= 2 Loop While (n >= 0) ' USAR la clave desde aquí ' llamada a FuncionX(Clave) k += 1 Loop While (k < s_MaxPermutaciones)
Equilicuá... si ya has visitado el enlace para saber lo que significa, tu pregunta sobra... Justo las líneas antes del bucle, señalé esto: If (.PermutacionInicialLng < 0) Then .PermutacionInicialLng = 0 If (.PermutacionInicialStr.Length > 0) Then ' FALTA: código para convertir la clave a la enésima permutación. ' es el proceso inverso al seguido en el algoritmo y debiera facilitarse como una función pública. ' k= EnesimaPermutacion(.PermutacionStr) ' La función que devolvería el índice de la permutación reclamada. Else k = .PermutacionInicialLng End If
Convertir una clave-apuesta (permutación) a un número indexado de permutación dentro de todas las permutaciones, es (como señalo en dicho texto) la operación inversa... Resulta tan obvio, que ni me molesté en hacerlo. En general con ese algoritmo (el primero de 4), la única forma de parar en una permutación específica para poder continuar desde donde se dejó en otro momento, exije precisamente convertir una permutación a su valor numérico (el enésimo en la permutación, justamente para luego sumar 1 y seguir generando permutaciones partiendo de ese valor)... Más arriba al comentar sobre ese algoritmo, describiía que es el más sencillo, pero también el más lento de los 4. Todas las permutaciones de la quiniela (3^14= 4'7millones), en éste equipo desde el que escribo, que data del 2008, las genera en 3'99 segundos, en tanto los otros algoritmos, los generan 2-3 órdenes más rápidos (cientos-miles de veces más rápido)... no se requieren multiplicaciones, divisiones, módulo... solo suma 1 para un único carácter (de toda la palabra) para generar la siguiente permutación. En los otros no puedo computar el tiempo exacto, siempre da 0 TICKS (frente a los casi 40millones de ticks). En definitiva, lo que te decía al principio es que esto es pura combinatoria, tratarlo como algo distinto, aleja el sentido matemático de un problema conocido, hacia algo que pueda parecer 'raro'... generar claves = generar las apuestas de la quiniela. Es lo mismo, solo cambia el alfabeto usado ("1X2", para la quiniela) y el tamaño de 'palabras' a generar (para la quiniela una palabra de 14 caracteres). Cambiando el nombre porque el dominio social sea diferente, no lo convierte en ningún problema nuevo ni distinto, de ahí que cuando señalaste que no habías encontrado 'fuentes', sin estar errado, no llega a ser cierto... es solo porque has buscado por un nombre específico, en vez del genérico del problema.
Si quieres hacer algo interesante sobre las quinielas (y de lo que no hay apenas literatura), te comento por ejemplo que intentes lograr cuántas y cuáles permutaciones para 4 partidos, son las mínimas necesarias para asegurar siempre que se aciertan al menos 3 (de los 4 partidos). Es decir que jugando x apuestas para 4 partidos, tengas asegurado (al menos) 3 aciertos... y cuáles son, o mejor dicho, como obtener las combinaciones de dichas apuestas... teniendo en cuanta que todas las permutaciones posibles para esas 4partidos, son al menos 3 triples (27 apuestas) y un partido fijo en las 27 apuestas, que lógicamente son costosas (los triples), ¿...se puede asegurar 3 aciertos con menos apuestas que las 27?... Esto es algo conocido, aunque te comento que existen muchas combinaciones (y curiosamente la ONLAE, solo contempla 1), más aún esto se puede ampliar a 5, 6, 7, etc... partidos, que lo hace todavía más interesante... Saludos. El uso que le has dado para generar claves me perece excelente y sinceramente a mi no se me había ocurrido, de hecho de haberseme ocurrido hubiera expandido más la idea en sí. Así que chapó por tí muy buena idea y buen trabajo. me parece admirable. Eso que dices que genera todas las variaciones de la quiniela en 3,99 segundos me recuerda a una discusión que tuve una vez con @Elektro no recuerdo de qué en la que él afirmaba que un determinado proceso ( que no recuerdo) lo hacía en pocos segundos mientras que a mí me tardaba minutos. La conclusión que yo llegué era a que era un tema de CPU, de medios informáticos, de hardware y no del código en sí. Aunque al final creo recordar no llegamos a un acuerdo. Si quieres hacer algo interesante sobre las quinielas (y de lo que no hay apenas literatura), te comento por ejemplo que intentes lograr cuántas y cuáles permutaciones para 4 partidos, son las mínimas necesarias para asegurar siempre que se aciertan al menos 3 (de los 4 partidos). Es decir que jugando x apuestas para 4 partidos, tengas asegurado (al menos) 3 aciertos... y cuáles son, o mejor dicho, como obtener las combinaciones de dichas apuestas... teniendo en cuanta que todas las permutaciones posibles para esas 4partidos, son al menos 3 triples (27 apuestas) y un partido fijo en las 27 apuestas, que lógicamente son costosas (los triples), ¿...se puede asegurar 3 aciertos con menos apuestas que las 27?...
Esto es algo conocido, aunque te comento que existen muchas combinaciones (y curiosamente la ONLAE, solo contempla 1), más aún esto se puede ampliar a 5, 6, 7, etc... partidos, que lo hace todavía más interesante...
Saludos.
Sí, ya desarrollé varios programas, de hecho estoy re-codificando y mejorando el último que está basado en un sistema propio el cual trata de garantizar y optimizar el acierto.
Me gustaría aclarar una cosa ya que con esto de variaciones, permutaciones y combianciones hay un poco lío. En la rama de las Matemáticas, la combinatoria, hay una especificación para cada caso. VARIACIONES son las formas de ordenar un grupo de elementos que pueden ser con repetición o sin repetición tomados de n en n. Ejemplo: Sin repetición: Elementos: A, B, C Tomados de dos en dos AC, AB, BC. Con repeticion Elementos: A, B, C de tres en tres AAA, AAB, AAC, BBB, CCC,... Tomados de 4 en 4 AAAB, ABBB, AAAC, .... PERMUTACIONES son variaciones en las que entran en cada grupo TODOS los elementos considerados. A, B, C, D ABCD ABDC ACBD ACDB ADBC ADCB BACD BADC BCAD BCDA BDAC BDCA CABD CADB CBAD CBDA CDAB CDBA DABC DACB DBAC DBCA DCAB DCBA 24 Permutaciones Las permutaciones con repetición son aquellas en los que están establecidos determinados elementos para permutarlos y que se repiten: Elementos: 2,2,2,4,4 Entonces sería todas las formas de permutar estos elementos de los cuales hay repetidos, pero que están condicionados el número de repeticiones, en este caso el dos, tres veces y el cuatro, dos veces. Y por último las COMBINACIONES. En este caso son aquellas combinaciones en las que se diferencian cada grupo cogidos de n en n, por ejemplo. A, B, C, D de 3 en 3: ABC, ABD, ACD pero no entraría CBA o BCA porque ya que se entiende estaría dentro del grupo ABC. Igualmente hay con Combinaciones sin repetición y con repetición. Esto lo aclaro porque en el caso de La Quiniela hablamos de VARIACIONES (con repetición) no permutaciones. Y si me equivoco corregidme el/la que sea.
Dicho lo anterior también aclarar que mi post está enfocado como "una curiosidad" (como especifico claramente si se lee) sobre el juego de La Quiniela en concreto y expongo ejemplo a modo de programación para aquellos quinialistas que sepan programar y deseen comprobarlo o usarlo en algún proyecto si cabe.
Estoy deseando estudiar tus códigos y cuando lo haga ya comentaré algo al respecto. Maldita sea, ya no tengo tanto tiempo como antes, a ver un día de estos o el fin de semana. Saludos
|
|
|
|
« Última modificación: 31 Mayo 2018, 01:25 am por okik »
|
 En línea
En línea
|
|
|
|
|
| Mensajes similares |
|
Asunto |
Iniciado por |
Respuestas |
Vistas |
Último mensaje |

|

|
El codigo de mi programa que pasa numeros binarios a base 10
« 1 2 »
Programación C/C++
|
elkiy
|
10
|
10,627
|
 29 Mayo 2013, 12:35 pm
29 Mayo 2013, 12:35 pm
por leosansan
|

|

|
Variaciones de Traceroute
Redes
|
Delacure Mihawk
|
2
|
3,357
|
 11 Diciembre 2013, 20:16 pm
11 Diciembre 2013, 20:16 pm
por el-brujo
|

|

|
Programar en C quiniela.
Programación C/C++
|
pepeluoman
|
6
|
5,895
|
 30 Diciembre 2013, 14:56 pm
30 Diciembre 2013, 14:56 pm
por dato000
|

|

|
Programar quiniela en C.
Programación General
|
pepeluoman
|
6
|
6,034
|
 23 Enero 2014, 22:54 pm
23 Enero 2014, 22:54 pm
por jdomgo3
|

|

|
VARIACIONES de n elementos tomados de m en m y sin repetición. VISUAL BASIC
Programación Visual Basic
|
iaycart
|
0
|
2,176
|
 4 Octubre 2015, 08:26 am
4 Octubre 2015, 08:26 am
por iaycart
|
 |








 Autor
Autor

 En línea
En línea




