Fuente:
http://elblogdeonce.blogspot.com.co/2017/07/parte-iii-vision-artificial.htmlAunque en la entrada anterior ([Parte II: visión artificial] Primeros pasos con OpenCV y Numpy) se habló un poco sobre numpy éste se merece una entrada completa (y más) debido a que el corazón de la visión artificial son las operaciones matriciales lo que hace de numpy una parte imprescindible incluso cuando usamos librerias que hacen gran parte del trabajo como OpenCV. El objetivo de ésta entrada es familiarizarnos un poco más con NumPy y así poder dejar sentado el terreno para comenzar a hacer visión artificial.
¿Cómo recorrer una matriz?Uno de los principales problemas/confusiones que he notado es a la hora de recorrer una matriz. La confusión es simple, suelen tratar a las matices como sistemas coordenados...
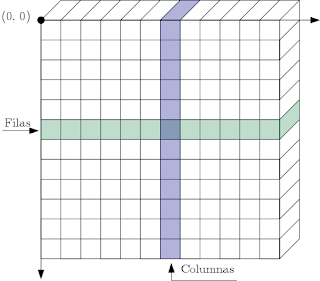
Figura: estructura de una matriz.
Por convención a cada sección horizontal de la matriz la llamamos una fila (verde) y a cada sección vertical una columna (azul). Además, la numeración de las filas y columnas comienza desde la esquina superior izquierda (el origen), las filas crecen hacía abajo y las columnas hacía la derecha.
Para acceder a un elemento, se debe especificar la fila y la columna (generalmente en ese orden exacto) donde se encuentra el elemento.
Y acá está el problema, cuando accedemos a un elemento de una matriz lo hacemos mediante dos coordenadas (fila, columna) por lo que debemos tener en cuenta que las filas nos mueven por la matriz verticalmente y que las columnas nos mueven por la matriz horizontalmente. Contrario a como nos movemos en un sistema coordenado donde por lo general la primer componente nos mueve horizontalmente (el eje de las x), y la segunda verticalmente (el eje de las y).
Tener esto en cuenta nos va a ahora MUCHOS dolores de cabeza en un futuro.
¿Cómo crear una matriz?Numpy nos proporciona varios métodos para crear matrices:
A partir de una lista
Para crear una matriz a partir de una lista tenemos el método numpy.array() que recibe como parametro una lista (que puede ser una lista de lista en el caso de las matrices)
>>> import numpy as np
>>> x = np.array([1, 2, 3]) # Vector
>>> x
array([1, 2, 3])
>>> X = np.array([[1, 2, 3], [4, 5, 6]]) # Matriz 2x3
>>> X
array([[1, 2, 3],
[4, 5, 6]])
Métodos predefinidosNumpy también nos proporciona unos métodos predefinidos para crear matrices, por ejemplo la matriz identidad, matrices de unos o de ceros:
>>> import numpy as np
>>> identidad = np.identity(3)
>>> identidad
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
>>> ceros = np.zeros((3, 3))
>>> ceros
array([[ 0., 0., 0.],
[ 0., 0., 0.],
[ 0., 0., 0.]])
>>> unos = np.ones((3, 3))
>>> unos
array([[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.]])
El método numpy.identity(n) genera la matriz identidad de dimensiones nxn
Los métodos numpy.zeros(tamaño), numpy.ones(tamaño) crean matrices de ceros y unos respectivamente.
¿Operaciones con matrices?Una de las cosas que más conmociona a las personas cuando se enfrentan por primer vez con numpy es que éste usa los mismos operadores de Python.
Así que veamos un repaso de éstos operadores:
Operador Uso Operación
+ a + b Suma
- a - b Resta
* a * b Multiplicación
/ a / b División
// a // b División entera
** a ** b Potencia
% a % b Módulo
< a < b Menor que
<= a <= b Menor o igual que
== a == b Igualdad
> a > b Mayor que
>= a >= b Mayor o igual que
!= a != b Distinto
Éstos son sólo algunos de los operadores de Python que además podemos usar con objetos de numpy. Esto se logra sobreescribiendo los operadores (algo de lo que hablaremos luego en una entrada aparte).
Hay dos cosas que debemos tener en cuenta:
- Al menos uno de los operandos debe ser un objeto numpy: Así es, no es necesario que los dos operandos sean objetos de numpy, basta con se sólo a, o sólo b sean objetos de numpy para que se pueda realizar la operación sin errores.
- Éstas operaciones son elemento a elemento: Acá tenemos dos casos:
- Tanto a como b son objetos de numpy: En este caso, las operaciones se realizan elemento a elemento, es decir, el primero de a con el primero de b, el segundo de a con el segundo de b... por lo que debemos tener en cuenta que tanto a, como b deben tener las mismas dimensiones.
- Hay un objeto de numpy y un número: En este caso, se aplica la operación deseada a toda la matriz con el número indicado.
El resultado va a ser una nueva matriz con el resultado de aplicar la operación indicada.
Si queremos la multiplicación habitual de matrices, a partir de Python 3.5 se introdujo el operador @ (PEP 465) que nos permite justo eso, realizar la multiplicación "real" entre matrices.
Un pequeño ejemplo
>>> import numpy as np
>>> a = np.ones((3, 3)) # Crea una matriz de unos 3x3
>>> a
array([[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.]])
>>> a = a * 2 # Multiplica cada componente de a por 2
>>> a
array([[ 2., 2., 2.],
[ 2., 2., 2.],
[ 2., 2., 2.]])
>>> b = np.ones((3, 3)) ** 5 # Eleva cada componente a la quintapotencia
>>> b
array([[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.]])
>>> b = b + 5 # Suma a cada componente de b 5
>>> b
array([[ 6., 6., 6.],
[ 6., 6., 6.],
[ 6., 6., 6.]])
>>> a @ b # Multiplicación matricial entre a y b
array([[ 36., 36., 36.],
[ 36., 36., 36.],
[ 36., 36., 36.]])
>>> b > 5 # Componentes mayores que 5
array([[ True, True, True],
[ True, True, True],
[ True, True, True]], dtype=bool)
>>> b < 3 # Componentes menores que 3
array([[False, False, False],
[False, False, False],
[False, False, False]], dtype=bool)
>>>
Indexing y slicingAl igual que las lista en Python, los objetos de numpy también soportan tanto el indexing, como el slicing.
IndexingEl indexing nos permite acceder a un elemento indicando sus coordenadas.
Si estamos trabajando con un vector (matriz con solo una columna o solo una fila) para acceder a un elemento sólo necesitamos su índice:
>>> import numpy as np
>>> x = np.array([1, 2, 3])
>>> x[0]
1
>>> x[1]
2
>>> x[-1]
3
>>>
El indexing para vectores funciona igual que para listas.
Si estamos trabajando con matrices, para acceder a un elemento, necesitamos dos coordenadas (a veces tres) la fila y la columna donde se encuentra el elemento que necesitamos:
>>> import numpy as np
>>> a = np.identity(3)
>>> a
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
>>> a[1, 1]
1.0
>>> a[1,-1]
0.0
>>> a[0,0]
1.0
Los índices negativos seleccionan un elemento comenzando desde el final del array, siendo -1 la posición del último elemento, -2 la del penultimo y así...
Es por eso que en el caso del array, x[-1] devuelve 3 ya que este es el último elemento del array; y en el caso de la matriz, a[1, -1] devuelve 0.0 ya que éste es el elemento que se encuentra en la primer fila y en la última columna.
SlicingEl slicing es una variación del indexing en la que en lugar de obtener un solo elemento, nos permite obtener un rango de elementos.
La sintaxis es igual a la del slicing para listas:
>>> import numpy as np
>>> x = np.arange(10)
>>> x
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> x[:5]
array([0, 1, 2, 3, 4])
>>> x[5:]
array([5, 6, 7, 8, 9])
>>> x[-1:0:-1]
array([9, 8, 7, 6, 5, 4, 3, 2, 1])
>>> x[-1:0:-2]
array([9, 7, 5, 3, 1])
Se indica el rango que se quiere obtener usando a:b (dos puntos) donde tanto a como b son enteros. a indica el inicio, si se omite, se toma 0 y b indica el final, si se omite, se toma -1.
Hay que tener en cuenta que el rango que devuelve el slicing va desde a hasta b - 1.
Además, hay un tercer parámetro opcional, también separado por : (dos puntos) que indica el paso (o salto).
Para las matrices la sintaxis es la misma, solo que debemos hacer el slicing tanto para las filas como para las columnas, separadas por una , (coma):
>>> import numpy as np
>>> a = np.identity(3)
>>> a
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
>>> a[1:, 1:]
array([[ 1., 0.],
[ 0., 1.]])
>>> a[:1, :1]
array([[ 1.]])
>>> a[:2, :2]
array([[ 1., 0.],
[ 0., 1.]])
>>>
Estos son solo ejemplos de indexing y slicing básicos, para ver operaciones más avanzadas y aclarar posibles dudas, referirse a la documentación oficial
Modificar los valores de una matrizPara modificar los valores de una matriz podemos hacerlo de a un solo elemento usando indexing, o de a varios elementos usando slicing.
Eso sí, siempre debemos tener en cuenta el tamaño de los datos que queremos escribir coincidan con el tamaño seleccionado en la matriz de destino.
>>> import numpy as np
>>> a = np.identity(3)
>>> a
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
>>> a[1, 1] = 10
>>> a
array([[ 1., 0., 0.],
[ 0., 10., 0.],
[ 0., 0., 1.]])
>>> a[1:, 1:] = np.ones((3, 3))
Traceback (most recent call last):
File "", line 1, in
ValueError: could not broadcast input array from shape (3,3) into shape (2,2)
>>> a[1:, 1:] = np.ones((2, 2))
>>> a
array([[ 1., 0., 0.],
[ 0., 1., 1.],
[ 0., 1., 1.]])
En éste caso, en la línea 12 ocurre un error porque estamos intentando asignar una matriz 3x3 a una zona de la matriz a de tamaño 2x2.
Uso de máscarasOtra forma de modificar los elementos de una matriz es mediante el uso de máscaras.
Una máscara es una matriz booleana (de falsos y verdaderos) donde las componentes verdaderas indican los elementos que van a ser modificados.
La máscara se pasa como si ésta fuera un índice:
>>> x = np.arange(25) # Crea un vector
>>> X = x.reshape(5, 5) # Convierte el vector a matriz de 5x5
>>> X
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]])
>>> mascara = (X % 2 == 0) # Genera máscara posición de los elementos pares
>>> mascara
array([[ True, False, True, False, True],
[False, True, False, True, False],
[ True, False, True, False, True],
[False, True, False, True, False],
[ True, False, True, False, True]], dtype=bool)
>>> X[mascara] = 0 # Cambia todos los pares por cero
>>> X
array([[ 0, 1, 0, 3, 0],
[ 5, 0, 7, 0, 9],
[ 0, 11, 0, 13, 0],
[15, 0, 17, 0, 19],
[ 0, 21, 0, 23, 0]])
¿Paso de matrices como valor o referencia?Otro de los inconvenientes (más que inconveniente es un dolor de trasero) en especial para quien apenas está comenzando con Python e incluso para los distraidos es que, a veces, despues de llamar a una función y de pasarle a esta una matriz sobre la que realizaremos una operación suceden cosas extrañas. (brujería podrian pensar algunos) y el culpable está en como Python pasa los parametros por valor y por referencia.
Parametros por valorDecimos que un parametro se pasa por valor cuando a una función se le pasa el valor (valga la redundancia) de una variable, o en otras palabras, una copia de una variable. Por lo tanto los cambios que se hagan sobre este parametro se hacen sobre la copia.
Parametros por referenciaDecimos que un parametro se pasa por referencia cuando a una función se le pasa la dirección en memoria de una variable en lugar de una copia de la variable. Por lo tanto los cambios que se hagan sobre este parametro, se hacen en la dirección de memoria a la que apunta y por lo tanto se hacen sobre la variable original.
Teniendo ésto en cuenta, ahora debemos comprender como toma Python los parametros por valor y por referencia.
Parametros por valor y referencia en PythonA Python no podemos especificarle explícitamente que valores queremos pasar por valor y cuales por referencia, en su lugar debemos recordar:
Los objetos mutables se pasan por referencia.
Los objetos inmutables se pasan por valor.
Los objetos mutables son aquellos que pueden cambiar su valor.
Los objetos inmutables son aquellos que no pueden cambiar su valor.
Aunque ésta definición no está completa (no es el objetivo de la entrada) es suficiente para comprender la "magía negra" que está por ocurrir. (Eso sí, teniendo en cuenta que las matrices de numpy son objetos mutables).
import numpy as np
def funcion(matriz):
matriz[1, 1] = 10
mi_matriz = np.ones((3, 3))
print("Antes de llamar la función:")
print(mi_matriz)
funcion(mi_matriz)
print("Después de llamar la función:")
print(mi_matriz)
Antes de llamar la función:
[[ 1. 1. 1.]
[ 1. 1. 1.]
[ 1. 1. 1.]]
Después de llamar la función:
[[ 1. 1. 1.]
[ 1. 10. 1.]
[ 1. 1. 1.]]
Ésto significa que los cambios que realizamos a la matriz (incluso con distinto nombre) dentro de la función son visibles (afectan a la variable fuera de la función) fuera de la función.
Si no queremos que esto suceda debemos crear explícitamente una copia de la matriz y pasar a la función ésta copia en lugar de la matriz original.
Para copiar una matriz, podemos hacer uso del método copy() que tienen los objetos de numpy:
import numpy as np
def funcion(matriz):
matriz[1, 1] = 10
mi_matriz = np.ones((3, 3))
print("Antes de llamar la función:")
print(mi_matriz)
funcion(mi_matriz.copy())
print("Después de llamar la función:")
print(mi_matriz)
Antes de llamar la función:
[[ 1. 1. 1.]
[ 1. 1. 1.]
[ 1. 1. 1.]]
Después de llamar la función:
[[ 1. 1. 1.]
[ 1. 1. 1.]
[ 1. 1. 1.]]
Ésta vez pasamos una copia de la matriz y no la matriz como tal, por lo que aunque se sigue pasando la copia de la matriz por referencia se está modificando la copia pero no la original.
Algunos métodos interesantes de numpynumpy.amin(matriz): Devuelve el menor elemento de la matriz.
numpy.amax(matriz): Devuelve el mayor elemento de la matriz.
numpy.arange(matriz): Similar a range()
numpy.sum(matriz): Suma todos los elementos de la matriz.
Algunos métodos de las matrices (objetos ndarray)matriz.ravel(): Devuelve un vector con los elementos de la matriz.
matriz.copy(): Copia la matriz.
matriz.reshape(tamaño): Cambia el tamaño de la matriz.
Referirse a la documentación para una lista completa de los métodos y propiedades: ir
Saludos!
Once.










 Autor
Autor



 En línea
En línea