Se me pide saber la ruta más corta desde el nodo O al nodo T. Los números que se muestran en las
aristas representan la distancia entre los nodos.
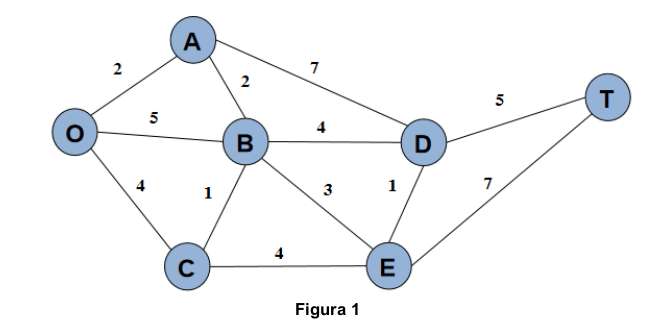
Debo elaborar un programa en C++ que encuentre la ruta más corta entre los nodos O y T utilizando el algoritmo de Dijkstra.
este es mi código
Código:
#include <iostream>
#include <queue>
#include <vector>
#define MAXV 100 // Maxima cantidad de vertices.
#define oo 0x3f3f3f3f // Nuestro valor infinito.
using namespace std;
struct Edge
{
int node; // El nodo destino de la arista.
int cost; // El costo de la arista.
Edge(int _node, int _cost) : node(_node), cost(_cost) {} // Constructor parametrizado.
Edge() : node(-1), cost(-1) {} // Constructor por defecto.
};
struct Graph
{
vector<Edge> G[MAXV]; // Lista de adyacencias.
int V; // Cantidad de vertices.
int E; // Cantidad de aristas.
};
struct State
{
int node; // El nodo actual.
int cost; // El costo del camino.
State(int _node, int _cost) : node(_node), cost(_cost) {} // Constructor parametrizado.
bool operator <(const State &b) const // Sobrecarga del operador de prioridad <.
{
return cost > b.cost;
}
};
int algoritmo(const int begin, const int end, const Graph graph)
{
priority_queue<State> pq; // La cola de prioridad.
vector<int> Dist(graph.V, oo); // La distancia hacia todos los vertices. Inicialmente para cada vertice su valor es infinito.
vector<bool> mark(graph.V, false); // Este arreglo nos permitira determinar los nodos procesados.
Dist[begin] = 0; // Valor inicial del vertice de partida.
pq.push(State(begin, 0)); // Agregamos el primer elemento, que no es mas que el vertice de partida.
while(!pq.empty()) // Mientras existan vertices por procesar.
{
State st = pq.top(); pq.pop(); // Se desencola el elemento minimo.
mark[st.node] = true; // Se marca el nodo como visitado.
if (st.node == end)
return st.cost; // Retornamos el valor del camino, hemos llegado al vertice destino.
int T = (int)graph.G[st.node].size();
for(int i = 0; i < T; ++i) // Se recorren las adyacencias de "a".
{
// Si no ha sido procesado el vertice "vi" y la distancia hacia "vi" es menor a la distancia
// en Dist entonces hemos encontrado un camino mas corto a "vi".
if (!mark[graph.G[st.node][i].node] && ((Dist[st.node] + graph.G[st.node][i].cost) < Dist[graph.G[st.node][i].node]))
{
Dist[graph.G[st.node][i].node] = st.cost + graph.G[st.node][i].cost;
pq.push(State(graph.G[st.node][i].node, st.cost + graph.G[st.node][i].cost));
}
}
}
return -1; // Si no se puede llegar al destino, retornar -1.
}
struct Programa
{
int V, E;
int comienzo, fin;
void definirGrafo(Graph& graph)
{
cout << "Ingrese Cantidad de Vertices: " << endl;
cin >> V;
cout << "Ingrese Cantidad de Aristas: " << endl;
cin >> E;
graph.V = V;
graph.E = E;
}
void cargarGrafo(Graph & graph)
{
for (int i = 0; i < E; ++i)
{
int Origen, Destino, Peso;
cout << "Ingrese Origen: " << endl;
cin >> Origen;
cout << "Ingrese Destino: " << endl;
cin >> Destino;
cout << "Ingrese Peso de la Arista: " << endl;
cin >> Peso;
// Insertamos la arista dos veces, ya que nuestro grafo es un grafo no dirigido.
graph.G[Origen].push_back(Edge(Destino, Peso));
graph.G[Destino].push_back(Edge(Origen, Peso));
}
}
void Dijkstra(Graph graph)
{
cout << "Ingrese Vertice Inicial: " << endl;
cin >> comienzo;
cout << "Ingrese Vertice Final: " << endl;
cin >> fin;
int n = algoritmo(comienzo, fin, graph);
cout << "Longitud del Camino mas Corto: " << n << endl;
}
};
int main()
{
bool out=false;
char salir;
Programa programa; //TAD
Graph graph; // Grafo.
cout << "Algoritmo de Dijkstra en C++" << endl;
while (!out)
{
programa.definirGrafo(graph); //Se define cantidad de vertices y cantidad de aristas del grafo
programa.cargarGrafo(graph); //Se cargan las aristas del Grafo
programa.Dijkstra(graph); //Se aplica el algoritmo de Dijkstra
//Desea Salir?
cout << "Salir? (S/N)" << endl;
cin >> salir;
if (salir == 'S')
{
out = true;
}
}
}
Mi duda es
Sera este el mejor enfoque para darle o ustedes creen que se puede cambiar algo
Muchas gracias a todos





 Autor
Autor


 En línea
En línea






