Autor
afirmaba que los francotiradores ajustaban su tiro porque la rotacion de la tierra afectaba su trayectoria...
entonces decidí echar lapiz al papel y calcular este efecto para ver que tanto puede afectar...
Bases teoricas:
Efecto coreolis: pueden buscar en wiki, pero lo describiré a mi forma... es la diferencia de velocidad dedivada por la rotacion de una figura, donde la parte interna gira a menor velocidad que la externa (imaginar un disco LP girando el centro se mueve a velocidad 0 y el borde a la velocidad de rotacion (giros/s) multiplicado por la circunsferencia... en una esfera aplica igual...
Disparo de francotirador: usando datos como que el tiro más lejano son unos 2.400m y que la velocidad de una bala .50 es ~1km/s
La tierra:
radio: 40.020km (en promedio, asumiré perfecta esfericidad y no me vengan que no, porque el diferencial está por debajo del 0.5%)
velocidad de rotacion: el efecto coreolis mismo nos dice que depende de la posicion así que la más alta es el ecuador, sabiendo que el radio es ese y que la tierra tarda 24horas en dar la vuelta...
1668km/h (redondeado) o 463m/s
ahora, sabemos que la velocidad depende del paralelo donde estés parado (no importa N o S), en la relacion
Citar
v=cos(paralelo)
(esta explicación la obviaré, si la quieren, comentenlo)¿Cuantos km es 1º de la tierra? 40.020km/360º = 111,16km/º
y la pregunta contraria, ¿cuantos grados representa 1km? 360º/40.020km = 0,01º/km (muy redondeado)
Calculos:
sabemos entonces que en el polo la velocidad de la tierra es
Citar
cos(90º)*463m/s=0m/s
y esta relacion conserva la "velocidad de cambio" de coseno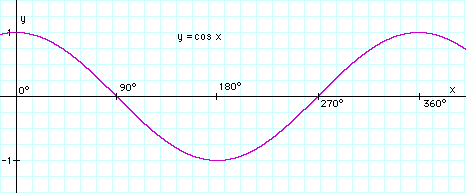
es decir, cerca de los 0º la diferencia de velocidad entre un punto y otro es muy alta, pero cerca de los 90º la diferencia tiende a 0
desmuestro numericamente
entre os grados 0 y 1 la diferencia fue de 0,1m/s, mientras que entre 89 y 90 fue de 8,1m/s
entonces, donde más podríamos ver esto es en el polo...
Caso 1:
un francotirador dispara su .50 acostado en el asta misma del polo norte a su objetivo a 2km exactamente al sur (no importa donde mire, será el sur XD)
sabiendo que el está en los 90º de latitud y su objetivo en los 89,98º de latitud
su objetivo que está quieto pero el conoce coreolis y sabe uqe se mueve 0,16m/s a la izquierda más rapdio que el y que su bala tardará 2 segundos en alcanzarlo, entonces tendrá que apuntar a 0,32m (32m) a la izquierda si no quiere fallar...
Caso 2:
un francotirador dispara su .50 en bagdag (~33ºN) exactamente al sur
sabiendo que el está en los 33º de latitud y su objetivo en los 32,98º de latitud, su objetivo se mueve a 0,088m/s más rapido que el, a 2 segundos su objetivo estará a 0.176m a su izquierda, debe ajustar 17,6cm para no fallar...
Conclusión:
si, el efecto coreolis afecta de una manera más o menos importante... este efecto es completamente anulado entre más al este/oeste se apunta (dah, si apunta al este está apuntando a la misma latitud)
aunque aclaremos algo, a 2km, incluso con una mira según lo que consigo militar, son 32mm a 10x es decir equivalente a un lente 320mm no es mucha la diferencia, más bien me sorprende que puedan ver a alguien... aquí pego un codigo para que vean como sería el zoom con una mira... tiene una imagen de muestra montada... si ven al hombre de naranja (en el centro de los rieles, muy lejos) no debe estar a mas de 500m y a 320mm ya la linea casi lo tapa completamente, a demás el sniper dudo que pueda predecir todas las corrientes de viento cruzantes en 2km... pero dejo mi envidia y el codigo (solo es copy/paste en un .html y listo, tiene defectos, no los pienso arreglar ya que es solo para demostrar este punto)
En línea
A ver si yo después del FP de DAM voy a por ing informática ^^ 
