Vamos a explicar en este artículo las funciones Hash. Seguramente todos hemos oido hablar de ellas, pero pocos tendrán claro lo que son realmente y como funcionan.
El artículo empezará desde cero e irá aumentando su nivel progresivamente hasta lograr una descripción total de este tipo de funciones.
Que es un Hash?
Si vamos a la definición de Wikipedia, nos dice "En informática, una función hash o algoritmo hash es una función para sumarizar o identificar probabilísticamente un gran conjunto de información, dando como resultado un conjunto imagen finito generalmente menor ..."
Muy bonito todo, pero como he dicho, voy a comenzar este artículo desde cero, paso a paso y despacito, para que todo el mundo pueda seguir por lo menos el principio.
Una función hash es un algoritmo matemático que nos da un resultado B al aplicarlo a un valor inicial A. Es como cualquier función matemática, por ejemplo la función raiz cuadrada nos daría como resultado 2 si se la aplicamos al número 4. E igual que cualquie función matemática tiene que actuar de tal forma y tiene que cumplir con ciertos criterios. No nos puede devolver cualquier cosa, lo que nos devuelva requiere que tenga ciertas propiedades para que podamos usarlo.
Que propiedades tienen que cumplir las funciones hash?
1- Sea cual sea la longitud del texto base A, la longitud de su hash resultante B siempre va a ser la misma. Por ejemplo, si la longitud de la salida B esta defiinida en 128 bits, si aplicamos una función hash a un A de 5 bits nos dará un B de 128 bits, y si se la aplicamos a un A de 380 millones de bits, nos dará un B de 128 bits igualmente.
2- Para cada entrada A, la función generará una salida B única. O lo que es lo mismo, es imposible que dos textos bases A y A' tengan un mismo hash B.
Según estas dos primeras propiedades, nos damos cuenta enseguida de la utilidad de las funciones de hash.
La más inmediata es usarla para generar un resumen de algo. De hecho, estas funciones se conocen también como funciones resumen. Un ejemplo real puede ser el del típico repositorio de documentos. Si alguien quiere almacenar digamos "Las_Aventuras_Del_Ingenioso.doc" cuyo contenido es El Quijote enterito, el sistema lo primero que tiene que hacer es revisar que no está previamente ya almacenado con el mismo o con otro nombre, por ejemplo "ElQuijote.doc". El sistema puede comparar letra a letras el documento de entrada con todos los docs de su BBDD para comprobar que no está, o puede comparar el resumen del documento de entrada con los resúmenes de los documentos de la BBDD, opción mucho más manejable y rápida.
Además, como la salida B es única para cada A, se puede usar también para verificar la integridad de A. Podemos ver que muchos programas incluyen su hash junto con su descarga, de esta forma, podemos verificar que el programa no ha sido modificado ni le han introducido un virus o ha sido troyanizado. Si a los bytes de una aplicación A les calculo el hash B y lo adjunto, cuando alguien modifique la aplicación A, al calcular de nuevo su hash su valor habrá cambiado y será distinto de B.
Podeis probar a calcular el md5 de un documento, luego modificais una simple coma del documento y calculais de nuevo el MD5. Vereis como ha cambiado completamente, aunque solo hemos modificado una simple coma.
3- Dado un texto base, es fácil y rápido (para un ordenador) calcular su número resumen.
4- Es imposible reconstruir el texto base a partir del número resumen.
Esto es lo que se conoce como One-Way hash functions. A partir del hash es imposible reconstruir el texto base.
Atención aquí !!!, no quiero que os lieis. Este es un punto que muchos no teneis claro. Solo hay que leer bien, a partir del hash B es imposible sacar el texto A, quiere decir no existe forma o es computacionalmente imposible, que mediante operaciones matemáticas inversas o no a las del algoritmo de hash, se llegue desde B al texto base.
Si os dais cuenta, esto es muy distinto que usar fuerza bruta. No tiene nada que ver. Con fuerza bruta le aplicamos la función de hash a diferentes textos hasta que obtenemos un hash similar al hash del texto que buscamos, con lo que por consecuencia tendremos el texto buscado.
Nuestra función hash.
Vamos a inventarnos un ejemplo para verlo claramente. Esto no podría tomarse como una función hash fiable porque es demasiado débil a ataques, pero nos vale como ejemplo gráfico por si no ha quedado del todo claro.
Esta función hash de nuestro ejemplo lo que hace es traducir cada caracter del texto A de entrada en su equivalente código ASCII, los agrupa de 3 en 3 y les aplica la función matemática (1º - 2º) * 3º.
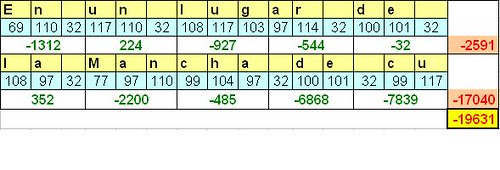
Como vemos, el valor de nuestra función hash aplicada al texto base A "En un lugar de la Mancha de cu" es -19631.
Cumple la propiedad 1, (o casi), con un poquito más de desarrollo se puede hacer que el tamaño del hash devuelto sea siempre el mismo.
Cumple con la 2, el valor del hash es único para cada texto. Si modificamos lo más mínimo la frase, el valor cambia.
Cumple con la 3 ya que es inmediato sacar el resultado y con la 4, ya que a partir del -19631 no se puede llegar al texto.
5. - No puede presentar Colisiones.
Que son las colisiones?
Según la primera caracteristica que hemos visto de las funciones hash, que nos dice que el tamaño del hash B resultante de A es siempre el mismo, deducimos que no puede cumplirse la segunda caracterisitca, que dice que el hash B tiene que ser único para cada A.
Por ejemplo, la función MD5 nos devuelve un hash de 128 bits. Para que cada hash equivalga a un unico texto base, tendría que existir solamente un texto por cada combinación del hash devuelto, o sea, tendría que haber solamente 2^128 textos distintos, lo cual no es cierto. Como textos distintos hay infinitos, podemos decir que hay infinitas posibilidades de que dos textos tengan el mismo hash.
Esto es lo que se conoce como colisiones.
Seguramente las hemos visto muchas veces sin darnos cuenta de que pasaba. Hay muchos sistemas que requieren contraseñas de uso, como pueden ser los sistemas de foros y demás, donde lo que se almacena no es la contraseña, sino el hash de esa contraseña. Esto no se hace con el propósito de resumir la contraseña, seguramente será mas corta que el hash generado, se hace con el propósito de que si alguien tiene acceso al almacén de contraseñas, o si alguien desensambla la aplicación proteguida, etc, no pueda ver la contraseña en plano y siga sin acceso (a no ser que la crackee por fuerza bruta si conoce el algoritmo de la función).
Os habeis encontrado alguna vez con algún programa que te pide una contraseña para acceder a algo, le metes el crackeador, y te da acceso pero sin darte la clave? Creo recordar que en el Excel95 o 97, el programa que desprotejía las hojas o las celdas, funcionaba así, te desproteguía la hoja pero no te daba la clave.
Eso es porque el algoritmo de la función hash que usan para las contraseñas es tan simple como el que hemos puesto de ejemplo, y tiene multiples colisiones muy fáciles de encontrar. Así que en vez de buscar la contraseña se buscaban colisiones a ese hash, contraseñas alternativas que tenían el mismo hash que la contraseña verdadera.
La fortaleza de una función hash requiere que estas colisiones sean las mínimas posibles y que encontrarlas sea lo más dificil posible.
Bien, hasta aquí llega la parte básica de las funciones hash. Se explica su funcionamiento general, sus propiedades y sus usos.
Ya no teneis excusa para preguntar como descifrar un hash, creo que ha quedado bien claro que los hashes no son un método de cifrado y que desde el resultado no se puede obtener el texto base más que por fuerza bruta.
Propiedades de una función hash con respecto a las colisiones.
Las propiedades que deben de tener las primitivas hash son:
1. Resistencia a la preimagen: One Way Hash Function. Como hemos dicho antes, significa que dada cualquier imagen, es computacionalmente imposible encontrar un mensaje x tal que h(x)=y. Otra forma como se conoce esta propiedad es que h sea de un solo sentido.
2. Resistencia a 2° preimagen: OWHF: Weak One Way Hash Function. Significa que dado x, es computacionalmente imposible encontrar una x’ tal que h(x)=h(x’). Otra forma de conocer esta propiedad es que h sea resistente a una colisión suave.
3. Resistencia a colisión: CRHF: Strong One Way Hash Function. Significa que es computacionalmente imposible encontrar dos diferentes mensajes x, x’ tal que h(x)=h(x’). Esta propiedad también se conoce como resistencia a colisión fuerte.
Vamos a poner unos ejemplos para ver la necesidad de estas propiedades:
Vamos a establecer un escenario de firma digital.
Un documento X se adjunta con su firma, que consiste en clacular el hash de X, h(X), y en cifrarlo, C(h(X)) con la clave privada del remitente o propietario.
Para verificar la integridad de X, el destinatario o la persona correspondiente descifra con la clave pública del propietario el C(h(X)) para obtener el h(X) inicial, calcula de nuevo el h(X) del documento y los compara. Si el h(X) inicial es igual al h(X) nuevo es que ese documento no ha sido modificado y que pertenece al firmante.
Si esa función de hash no tiene resintencia a una 2ª preimagen, un atacante C que podría encontrar un mensaje X' tal que h(X') = h(X), y reclamar que el documento firmado no es X sino X'.
O imaginemos que C tiene que presentar para firmar por un tercero un documento X, y a la vez redacta otro documento Y. Si la función hash no tiene resistencia a las colisiones, C puede añadir información basura a X e Y (X' e Y') de forma que h(X+X') = h(Y+Y'). Entonces el que firme X también está firmando Y.
Por último si (e,n) es la clave pública RSA de A, C puede elegir aleatoriamente un y y calcular z = ye mod n, y reclamar que y es la firma de z, si C puede encontrar una preimagen x tal que z = h(x), donde x es importante para A. Esto es evitable si h es resistente a preimagen.
Algoritmo MD5
El algoritmo MD5 realiza las siguientes operaciones:
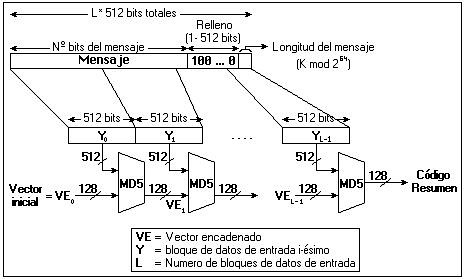
1. Adición de bits de relleno:
El mensaje es rellenado o ampliado para que su longitud en bits sea congruente a 448 módulo 512. Esto debe ser así puesto que hay que reservar 64 bits para la adición de la longitud del mensaje en el próximo paso. Así pues, si no se llega a la anterior congruencia, se añadirá el relleno, consistente en un bit ‘1’ seguido de tantos bits ‘0’ como se precisen.
La razón de porqué un uno seguido de ceros se debe que si se emplea sólo relleno con un valor (por ejemplo todo ceros) el proceso no sería reversible a la hora de eliminar dicho relleno.
De todas maneras, siempre se realiza esta operación de relleno, aunque la longitud del mensaje ya sea congruente a 448 en módulo 512. Por ello, se añadirán como mínimo 1 bit de relleno, y como máximo 512 bits. Obsérvese la siguiente figura:
2. Adición de representación binaria de longitud del mensaje:
Posteriormente se añade al mensaje (con el relleno realizado) una representación de la longitud del mensaje antes de ser rellenado. Dicha representación tendrá una longitud de 64 bits (16 palabras de 32 bits, es decir, dos enteros de 4 octetos cada uno). En el caso de que el mensaje sea mayor de bits, sólo se tendrán en cuenta los 64 bits menos representativos, que es lo mismo que decir que esta representación de la longitud del mensaje está realizada en módulo.
El mensaje tiene ahora un número de bits múltiplo de 512, por lo que habrá un número entero de palabras de 32 bits (enteros de 4 octetos), concretamente 512 / 32 = 16, de lo que se puede concluir que si hay b bloques de 512 bits cada uno que forman el mensaje, entonces el mensaje tendrá n palabras de 32 bits: n = 16 * b
3. Inicializar buffer MD:
Para poder calcular el valor hash o resumen se necesita tener un buffer de 4 palabras de 32 bits (A, B, C, D), pero antes de comenzar con el proceso se los ha de inicializar con algún valor determinado, que Rivest establece:
Palabra A = 01 23 45 67 67 45 23 01
Palabra B = 89 ab cd ef ef cd ab 89
Palabra C = fe dc ba 98 98 ba dc fe
Palabra D = 76 54 32 10 10 32 54 76
En la primera columna los valores hexadecimales están ordenados de modo que los valores menos significativos aparecen en primer lugar (notación empleada por Rivest en la implementación de este algoritmo), y en la segunda los valores más significativos están a la izquierda (posiciones más altas de la memoria en Intel 80xxx)
La razón de ver estas formas de representar los mismos valores se debe a intentar evitar confusiones, pues en función del tipo y arquitectura de la máquina sobre la que ha de trabajar el algoritmo, este sufrirá adaptaciones en dichos valores al realizar la implementación. Ello es debido a las distintas formas en que se almacenan los datos en memoria en las distintas arquitecturas (Intel, Sun, Sparc, ...)
Los algoritmos MD4 y MD5 están pensados para facilitar su implementación en arquitecturas denominadas little-endian. Este formato asume que el byte menos significativo de una palabra se almacena en la posición más baja, y el byte más significativo en la parte más alta. Es el formato que emplean los procesadores Intel 80xxx que integran los PC domésticos.
4. Procesar el mensaje en bloques de 512 bits:
Esta es la parte central del algoritmo. Aquí se definen las cuatro funciones que se emplearán en las cuatro vueltas que se aplicarán sobre cada bloque. Véase la siguiente figura:
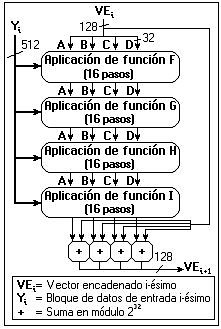
Estas cuatro funciones reciben como parámetros de entrada tres palabras de 32 bits cada una (tres enteros de 4 bytes de longitud) y devuelven como salida una. Son las siguientes:
F(X, Y, Z) = (X and Y) or ((not X) and Z)
G(X, Y, Z) = (X and Z) or (Y and (not Z))
H(X, Y, Z) = X Y Z
I(X, Y, Z) = Y (X or (not Z))
Donde F funciona como una sentencia condicional if en programación tradicional: Sí X = 1 entonces Y será 1 de lo contrario Z será 1.
G también funciona de manera condicional como F: Si Z = 1 entonces X será 1 de lo contrario Y será 1.
H simplemente realiza la operación OR-Exclusiva (XOR) de X, Y y Z.
I realiza la operación XOR con X si es 1 o si Z es 0.
Por otro lado MD5 no utiliza las constantes (‘magic’ constants) que se empleaban en MD4. En su lugar se emplea una tabla de 64 elementos construida a partir de la función trigonométrica seno. Sea T el elemento i-ésimo de dicha tabla, que será igual a la parte entera de 4294967296 veces abs(sen(i)), donde i está expresada en radianes. Puesto que hay que realizar 16 pasos en cada una de las cuatro vueltas, es decir, 64 operaciones, la idea es usar una constante de la anterior tabla para cada vuelta.
5. Recoger el valor hash de salida:
El valor hash de salida se obtiene de los registros A, B, C y D donde el octeto más representativo es D y el que menos A.
Ataques
Ataque de Cumpleaños.
El ataque más conocido (de fuerza bruta) a una función hash es conocido como "birthday attack" y se basa en la siguiente paradoja.
Cual es la cantida de personas que hay que poner en una habitación para que la probabilidad de que el cumpleaños de una de ellas sea el mismo día que el mio?
Debemos calcular un tal que n(1/365) > 0.5, luego n > 182.
Sin embargo, cual sería la cantidad de personas necesarias para que dos cualesquiera de ellas cumplan años el mismo dia?
Cada pareja tiene un probabilidad de 1/365, y en un grupo de n personas hay n(n-1)/2 parejas diferentes, luego
(n(n-1)/2)(1/365) > 0.5
Esto se cumple si n>23, una cantidad sorprendente mas pequeña que 182.
La consecuencia de esta paradoja es que aunque es muy dificil dado un x calcular un x' tal que h(x) = h(x'), resulta mucho más fácil buscar dos valores aleatorios x y x' tal que h(x) = h(x´).
Esto en la práctica significa que un hash de n bits permitiría una colisión de 2º preimagen o débil una vez de cada 2^n, pero producirá una colisión fuerte una vez de cada 2^(n/2).
En el caso de un hash de 64 bits necesitaríamos 2^64 mensajes dado un x para obtener el x', pero bastaría generar 2^32 mensajes aleatorios para que aparecieran dos con el mismo hash. El primer ataque nos llevaría 600.000 años en un ordenador que generara un millón de mensajes por segundo, mientras que el segundo apenas necesitaría unas horas.
Ataque Wang-Yin-Yu o Ataque chino
Supongo que muchos habreis leído actualmente que las funciones hash MD5 y SHA1 han sido rotas por un grupo de matemáticos chinos y que ya no sirven para nada y demás.
Vamos a tratar de explicar esto para que todo el mundo pueda evaluar el grado de ruptura de estas funciones, porque se habla mucho de esto en los foros, pero no se evalua hasta que punto nos afecta.
Como hemos visto en el Ataque de Cumpleaños, para encontrar dos mensajes X y X' aleatorios que tengan el mismo SHA-1 (160 bits) por ejemplo, por fuerza bruta se necesitarían generar 2^(160/2) mensajes.
Pues bien, este grupo de matemáticos ha descubierto un sistema que permite hacer esto con un esfuerzo menor que por fuerza bruta.
En concreto para el SHA1, pueden encontrar una "colisión de cumpleaños" con un esfuerzo equivalente a 2^69 operaciones hash, en vez de las 2^80 requeridas por fuerza bruta.
Como podemos ver, este es una ataque contra las colisiones fuertes, pero no contra las colisiones de 2 preimagen, a las cuales no afecta. Si alguien quiere generar un mensaje x' que tenga el mismo SHA1 que un mensaje x ya existente, tiene que seguir generando 2^160 mensajes para conseguirlo.
Y aunque el "ataque de cumpleaños" contra SHA1 se ha vuelto 2000 veces más rápido, sigue siendo del orden de 10.000 veces más dificil que un ataque contra un DES, que no está al alcance de todo el mundo.
Ahora bien, existen casos en que las implicaciones son importantes.
Imaginemos que redacto un contrato A de venta de un inmueble en word, al cual le adjunto varios jpgs con fotografías del inmueble.
Al mismo tiempo genero un contrato alternativo A' con las mismas fotos pero modificando el precio de venta a mi favor.
Es prácticamente imposible que el h(A) = h(A').
Sin embargo puedo crear múltiples versiones de A y de A', modificando aleatoriamente bits de las fotografías (se podría hacer modificando el texto, añadiendo espacios, cambiando cosas no significativas, etc, pero quedaría un texto muy sucio y se notaría la "trampa". Pero modificando bits de las fotografías como mucho perderé algo de calidad), hasta conseguir dos versiones que tengan el mismo hash.
Le presento al comprador la versión de A, acepta las condiciones y lo firma electrónicamente. Cambio la variante de A por la de A' y ya tengo un contrato legal de compraventa firmado con unas condiciones distintas de lo establecido.
Si la función hash que se va a utilizar para realizar la firma es por ejemplo un SHA1, mediante el ataque tri-chino tendré que generar 2^69 variantes de A y 2^69 variantes de A', que como hemos visto antes, aunque no esté al alcance de cualquiera, es factible.
Pero si la función hash es por ejemplo un MD5, solo tendré que generar 2^32 variantes de A y 2^32 variantes de A', que está al alcance de cualquier PC.
Ataque Multicolision de Joux-Wang.
Si nos fijamos en el funcionamiento del algoritmo MD5, vemos el mensaje se divide en bloques de 512 bits. El primer bloque es "hasheado" usando como parámetro el vector de inicialización y dando como resultado otro vector de 128 bits, que sirve como inicialización para el siguiente bloque de 512 bits, y así sucesivamente.
Entonces se hace obvio que si tengo dos n*bloques A y B, siendo A != B, que cumplen que MD5(A) = MD5(B), si les añado un "payload" Q, entonces MD5(A+Q) = MD5(B+Q).
Como posible prueba de concepto de esto os remito a un artículo de Eduardo Díaz, http://www.codeproject.com/dotnet/HackingMd5.asp.
El desarrollo ahí mostrado como ejemplo, se basa en una aplicación que ejecuta archivos en un formato propietario de distribución. Tenemos un ejecutable goodexe.exe que antes de distribuirlo se convierte a su formato .bin, y un programa "extractor" que ejecuta ese .bin.
También tiene un ejecutable devilexe.exe que se supone que es el malware.
Lo que hace su aplicación es, teniendo un vector A y otro B tal que MD5(A) = MD5(B), genera el good.bin haciendo A + goodexe.exe + evilexe.exe, y genera el evil.bin haciendo B + goodeexe.exe + evilexe.exe. De esta forma, MD5(good.bin) = MD5(evil.bin).
Luego el programa extractor, mirando si el .bin tiene A o tiene B, ejecuta goodexe o evilexe.
De esta forma puedes colgar good.bin en la red, y mas tarde sustituirlo por evil.bin (previamente renombrado por supuesto).
Como los MD5 son iguales, nadie se dudará, y ejecutará otro programa distinto.
Personalmente no le veo utilidad a este ejemplo, es como distribuir un troyano solo que la fecha de activación la decides tú al cambiar de versión.
"La historia de Alicia y su jefe"
Hay otro ejemplo que si es más interesante.
Aquí podeis ver dos cartas en PostScript distintas dentro del mismo contexto cuyo MD5 es el mismo en ambas:
http://www.cits.rub.de/MD5Collisions/
Al firmar una, que es una carta de recomendación normal y corriente, estás firmando la otra, que es una carta que te da acceso a unos secretos.
Los creadores de estas cartas no dan detalles técnicos a cerca de como se hace esto, aunque dicen que están preparando una documentación que lo explica.
Pero a nosotros no nos gusta esperar, así que detallamos el procedimiento en exclusiva.
Si editamos ambos .ps, vemos que el codigo es algo tal que asi:
Código:
%!PS-Adobe-1.0
%%BoundingBox: 0 0 612 792
(caracteres raros)(caracteres raros)eq{/Times-Roman findfont 20 scalefont setfont
300 700 moveto (Julius. Caesar) show
.
.
}{/Times-Roman findfont 20 scalefont setfont
300 700 moveto (Julius. Caesar) show
.
.
}ifelse
showpage
Quizás os despiste un poco porque el código está en notación polaca inversa, pero si nos fijamos en la línea de los caracteres raros, lo que está haciendo es comparar todo lo que hay dentro del primer paréntesis con lo que hay dentro del segundo.
Si son iguales devuelve True, y se ejecuta el código del primer bloque {}, que es el que corresponde al de la carta de recomendación, y si no son iguales ejecuta el código del siguiente bloque {}, que es la carta que da poderes.
Ahora abrimos ambos .ps con un editor hexadecimal y nos fijamos en como está la estructura diviéndola en bloques de 64 bytes.
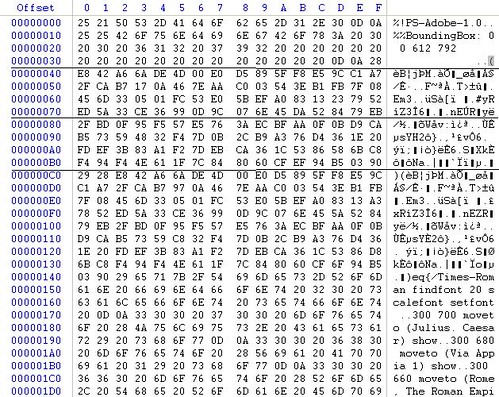
Order.ps
[/size]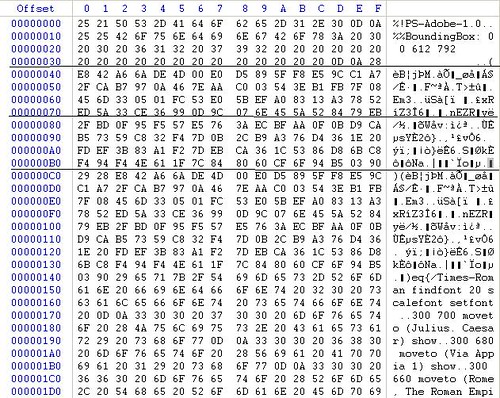
letter_of_rec.ps
[/size]Por qué 64 bytes? Porque como hemos dicho antes, el algoritmo MD5 va "hasheando" de 512 en 512 bits (64 bytes).
Así que vemos que el primer bloque de 64 bytes es común en ambos .ps, dado que es la cabecera, que ha sido retocada convenientemente para que ocupe exactamente eso.
Bien, y también vemos que los siguientes dos bloques de 64 bytes corresponden exactamente a los caracteres del primer paréntesis.
Estos dos bloques difieren de un ps a otro.
A partir del 4 bloque, ya todo es común para ambos .ps.
Ahora ya todo se ve más claro.
Han montado la cabecera Cab para que ocupe 64 bytes. Luego han creado dos versiones A y B añadiendo 128 bytes aleatoriamente buscando una colisión tal que MD5(Cab + A) = MD5(Cab + B).
En este punto, como el resto del código es igual para ambos documentos, ambos documentos compartiran hash, así que lo que se hace es mirar si el documento tiene A o B para enseñar una carta o la otra.
Estado actual de las funciones Hash.
La función hash MD4 está totalmente rota y descatalogada, de hecho existen algoritmos que encuentran colisiones en pocos segundos.
Para el uso del MD5 hay que tomar ciertas precauciones, pero cualquiera que se haya leido este artículo está capacitado para tomarlas. Lo mejor es no usarlo, pero si no nos queda más remedio, usándolo con cuidado es perfectamente seguro. Por ejemplo no firmeis nada usando MD5 si el que redacta el documento a firmar es parte interesada, o antes de firmarlo modificad algo del documento, o guardad copia, etc.
Para SHA1, yo no diría como se dice en muchos sitios que el edificio está en llamas y que estamos perdidos. Lo único es que las alarmas suenan, aunque no veamos aún el humo, y lo prudente es ir hacia la salida de emergencia, pero no hace falta correr ni que cunda el pánico. Pero tampoco hay que quedarse en el sitio, porque los ataques criptoanalíticos cada día mejoran, y cada será más fácil y rápido.
La solución que se está dando a esta problemática es ir incrementando el tamaño de los hashes. PGP ya usa SHA256, etc. Pero es solamente un parche. Estos algoritmos son todos monocultivo, y dándoles mas bits solo incrementas el esfuerzo para encontrar colisiones. Pero según avancen los métodos de criptoanálisis y la potencia de los ordenadores, se irán recortando los tiempos, y estaremos en las mismas.
El punto más crítico es el legal. Todo lo que se firme con un certificado legal o con el futuro DNI electrónico, tiene el mismo valor que una firma manuscrita.
Esta consideración legal se sustenta entre otras cosas en que el algoritmo de hash de la firma funciona como tiene que ser y que el hash resultante es único para el texto firmado.
Si un sistema no puede garantizar que es tal el documento que has firmado, y que no hay posibilidad de que te hayan dado el cambiazo con otro documento que tiene el mismo hash, todos los documentos firmados por esa aplicación no serán legales.
Teneis el caso de las fotografias de tráfico de Australia sin ir más lejos:
http://www.hispasec.com/unaaldia/2489
Solución? Muy simple. Usando dobles hashes.
La gente no le da la importancia que tiene al problema de las colisiones, y si se la dan, por ejemplo PHP, no lo solucionan como es debido.
Si para firmar algo en vez de cifrar el MD5 o el SHA1 o el SHA256 del documento, se cifrara una concatenación por ejemplo de MD5+SHA1, habría que buscar una colisión doble para conseguir un documento alternativo, lo que actualmente es imposible.
Si teneis que usar las firmas electrónicas para vuestros documentos, y se van a firmar por ejemplo usando MD5, añadidles un campo estilo fingerprint con el hash del documento en SHA1.





 Autor
Autor



 En línea
En línea












